AdaBoost 를 통한 Boosting 개념 이해

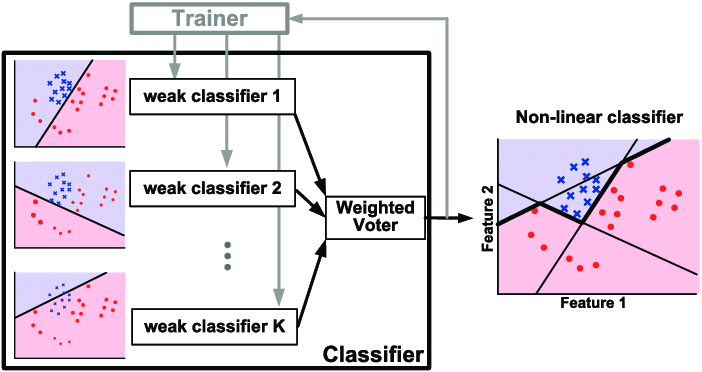
앙상블 학습

앙상블 학습이란 트리 계열 모델 뿐만이 아니라 신경망, 회귀식 등 다양에 형태의 모델에 적용할 수 있다. 예측력이 낮지만 연산 부담 또한 적은 여러개의 모델을 조합해, 하나의 복잡한 모델보다 향상된 성능의 아웃풋을 내는 것을 목적으로 하고 있는데, 특히 Kaggle 등의 데이터 대회에서 트리 계열의 앙상블 학습법은 비신경망 모델링 중 최상위권의 성능을 보여주고있다.

앙상블 학습법은 크게 Bagging, Stacking, Boosting 으로 분류할 수 있으며, 이 중 가장 복잡하지만 성능이 높은 Boosting 알고리즘을 초기 알고리즘인 AdaBoost 를 통해 설명하고자 한다.

Bagging & Stacking

Bagging 알고리즘은 homogenous 한 여러 모델의 조합이다. 여기서 homogenous 라 함은 모델의 종류가 하나인, 예를 들어 결정 트리만으로 이루어진 앙상블 모델 등을 의미하며, 개별 모델의 학습은 독립적으로 이루어지게 된다. 널리 알려진 랜덤 포레스트 알고리즘은 이러한 Bagging 알고리즘에 데이터 샘플링을 적용한 경우이다.

Stacking 알고리즘은 이와 다르게 heterogenous, 즉 서로 다른 종류의 모델의 독립적인 조합으로 설명할 수 있다. GLM, 신경망, Bagging 앙상블 모델 등을 조합한 모델을 그 예시로 들 수 있으며, 따라서 모델의 의미를 직관적으로 해석하기에 많은 어려움이 따를 수 있다.

Boosting

Boosting 알고리즘은 개별 모델의 학습이 이전 모델의 성능에 따라 순차적으로 이루어지는 앙상블 학습 방식이다. 따라서 각 모델의 학습은 독립적으로 이루어지지 않으며, 대표적인 예시로 AdaBoost, Gradient Boosting 등을 들 수 있다.

AdaBoost

AdaBoost (Adaptive Boosting) 은 1995년 학계에 공개된 이진 분류 모델이다. 유사한 트리 기반 모델인 랜덤 포레스트 알고리즘 또한 같은 연도에 공개되었는데, 이 글에서는 유명한 StatQuest 비디오를 참고하여 AdaBoost, 랜덤 포레스트 간의 차이점을 기반으로 개념을 소개하고자 한다. 글을 읽기 전 결정 트리, 랜덤 포레스트 등의 개념을 이해하고 있다는 것을 전제로 하고 있다.

AdaBoost 알고리즘을 랜덤 포레스트와 구분짓는 중요한 포인트는 다음과 같이 정리할 수 있다.

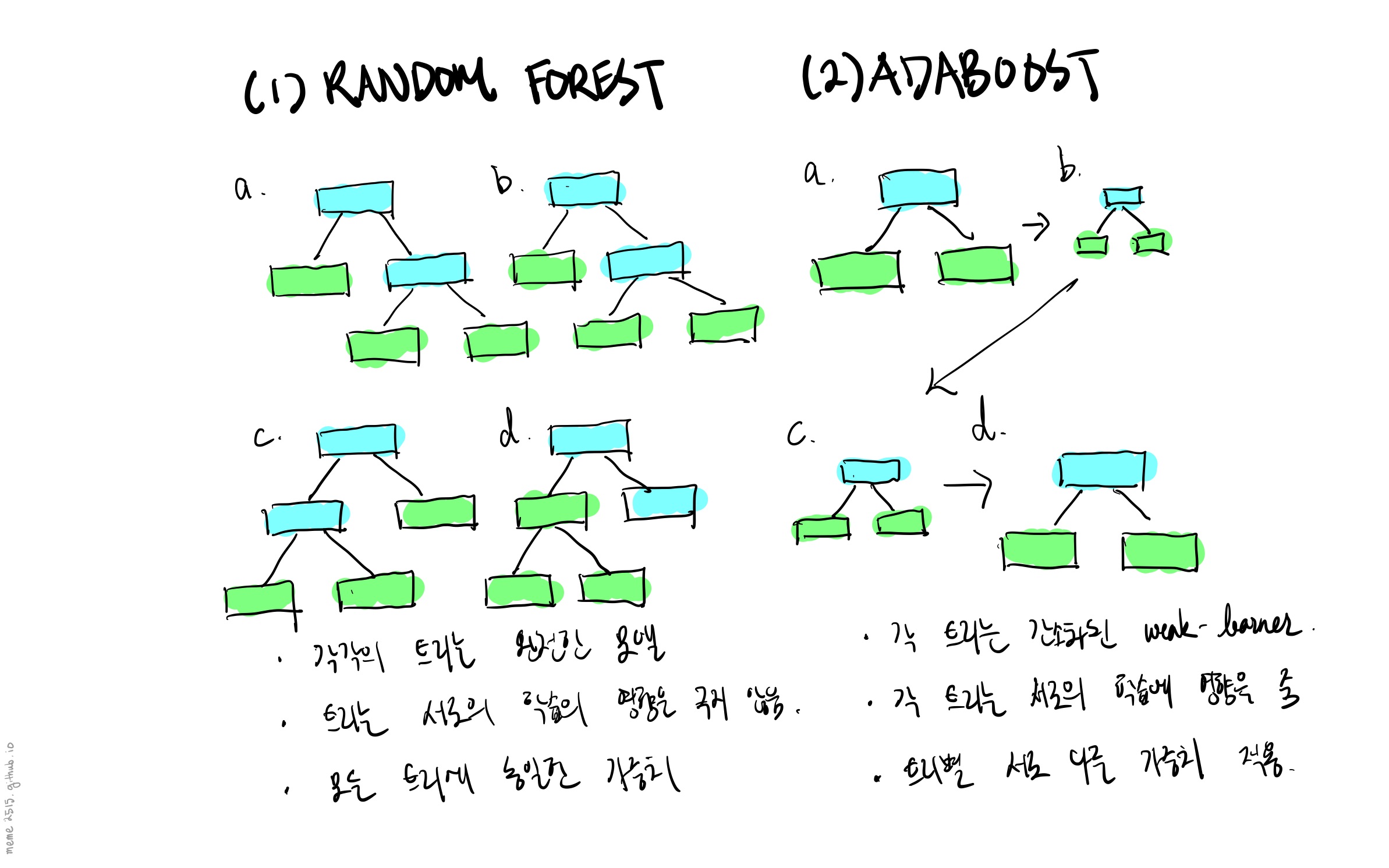
랜덤 포레스트의 각 트리는 그 자체로 하나의 완전한 결정 트리 모델인 반면, AdaBoost의 각 트리는 Stump 라는, 한 개 특성을 대상으로 한 번의 분류만을 수행하는 weak learner 이다.
랜덤 포레스트 모델은 각 트리에 동일한 가중치를 적용해 최종 분류값를 결정하는 반면, AdaBoost 는 트리마다 서로 다른 가중치를 적용한다.
랜덤 포레스트의 트리는 서로의 학습에 영향을 끼치지않는, 독립적인 모델인 반면 AdaBoost의 각 트리는 이전 모델의 오분류 케이스를 기반으로, 순차적으로 학습된다.


Fig 1. Random Forest 와 AdaBoost 의 차이점

Stump 생성

결정 트리 한 개 학습 사이클과 동일하다고 생각하면 된다. 우선 각 특성 마다 지니 불순도와 CART 알고리즘을 기반으로 한 최적의 임곗값을 특정한 후, 특성 별 모델 중 지니 불순도가 가장 낮은 특성/모델을 기반으로 Stump 를 생성하게 된다. 한 개 특성을 대상으로 한 번의 분류만을 수행하기 때문에 (1) 키가 176 보다 크다, (2) 몸무게가 50kg 이상이다 등의 아주 기초적인 분류만을 수행하게 된다.

Amount of Say

Stump 를 생성한 직후에는 앙상블 모델에 해당 Stump 가 기여할 가중치, Amount of Say (AoS) 를 부여하게된다. 이러한 개별 모델의 AoS 는 해당 모델의 분류 정확도에 기반하게 되며, 여기서 분류 정확도란 지니 계수가 아닌 오분류된 데이터 샘플의 가중치 합, Total Error 이다. 데이터의 가중치는 AoS 와는 다른 개념이다. Stump 가 분류하기 어려워하는 데이터를 특정한 후, 이에 더욱 큰 가중치를 부여해 이후 학습에서 강조하는 역할을 한다. 모든 데이터의 가중치 합은 항상 1 이어야 하며, 최초 학습 시 모든 데이터는 동일한 가중치를 부여 받는다.

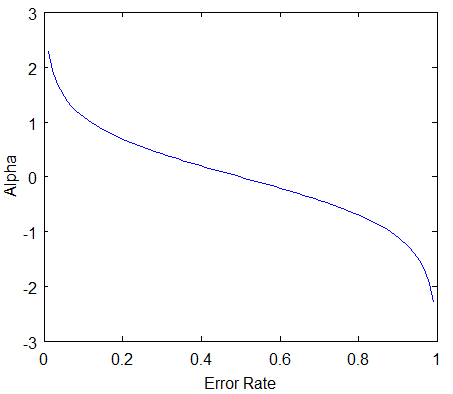
AoS 를 구하는 수식은 다음과 같이 정리할 수 있으며, 마치 sigmoid 함수를 90도 돌려놓은 듯한 모양을 가지고있다. 따라서 분류 정확도가 낮아지거나, 높아질수록 AoS 값은 극단적으로 변하게된다.

$$ \text{AoS} = \frac{1}{2} \text{log} (\frac{1 - \text{total error}}{\text{total error}}) $$


Fig 2. Amount of Say

오분류된 데이터를 강조한다는 룰에 따라 데이터 별 가중치는 잘못 분류된 경우 증가하고, 제대로 분류된 경우 감소하게 된다.

오분류된 데이터의 가중치를 증가시키는 경우, 새로운 가중치는 다음과 같이 정의된다.

$$ \text{새로운 샘플 가중치} = \text{현재 샘플 가중치} \cdot e^{AoS} $$

반대로 정분류된 데이터의 가중치를 감소시키는 경우, 새로운 가중치는 다음과 같이 정의된다.

$$ \text{새로운 샘플 가중치} = \text{현재 샘플 가중치} \cdot e^{-AoS} $$

수식의 의미를 해석하자면, AoS 가 높은 경우엔 (즉 Stump 의 분류 성능이 좋은 경우) 정분류된 데이터는 해결된 문제라고 판단해 더욱 작은 가중치를 부여하고, 특정된 오분류 데이터에 더욱 높은 가중치를 부여해 이후 해결하는 과정이라고 볼 수 있다. 또한 이렇게 업데이트 된 데이터 가중치는 정규화를 통해 그 합이 1 이 되도록 유지한다.

의사 결정

Amount of Say 와 Stump 의 개념을 이해했다면 AdaBoost 모델이 의사 결정을 내리는 과정을 쉽게 이해할 수 있다. 일정 개수의 Stump 가 생성된 후, AdaBoost 는 test 케이스에 대해 A 로 분류한 Stump 의 AoS 합과 B 로 분류한 Stump 의 AoS 합을 비교하여 더욱 큰 AoS 를 가진 클래스로 test 케이스를 분류한다.

랜덤 포레스트와 Bagging 알고리즘의 관계와 같이 AdaBoost 는 Boosting 알고리즘의 한 케이스에 불과하며, 순차적인 학습의 개념을 이해하기 위해 해당 글이 제시한 예시로 보면 좋을 것 같다. 나아가 이후에 LightGBM, XGBoost 와 같은 Gradient Boosting 알고리즘 또한 정리해 볼 예정이다.