인과추론 (Causal Inference) 개요

Introduction

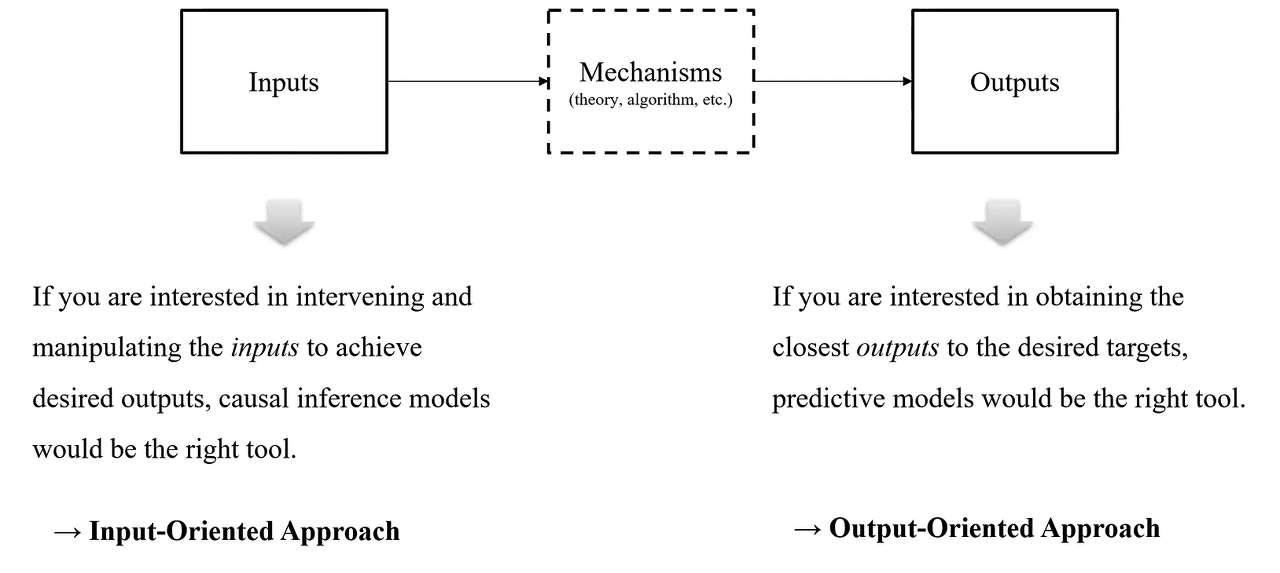
인과추론이란 최종적인 결과값에 영향을 주는 독립변수를 파악해, 이를 조절하는 것에 목적을 두며 예측과제와 상반된 목적을 가진다.


Fig 1. Prediction vs. Causal Inference, 벌꿀오소리의 공부 일지

인과추론과 예측 과제는 다른 목적을 가지지만 경우에 따라 (ex. 모델링을 위한 변수 선정 과정에서 인과추론 방법론 활용 등) 상호 보완적인 관계를 가질 수 있다.
- 인과추론과 예측 과제는 인풋 -> 모델 -> 아웃풋 이라는 간단한 파이프라인 내에서 최종적인 관심사가 다를뿐, 서로 밀접한 관계를 맺는다.
인과추론 모델 또한 한계점을 가지기 때문에 결과를 절대적인 답으로 볼 수는 없다. 다만 합리적이고 구체적인 증거를 기반으로 주장할 수 있는 근거를 제시한다.


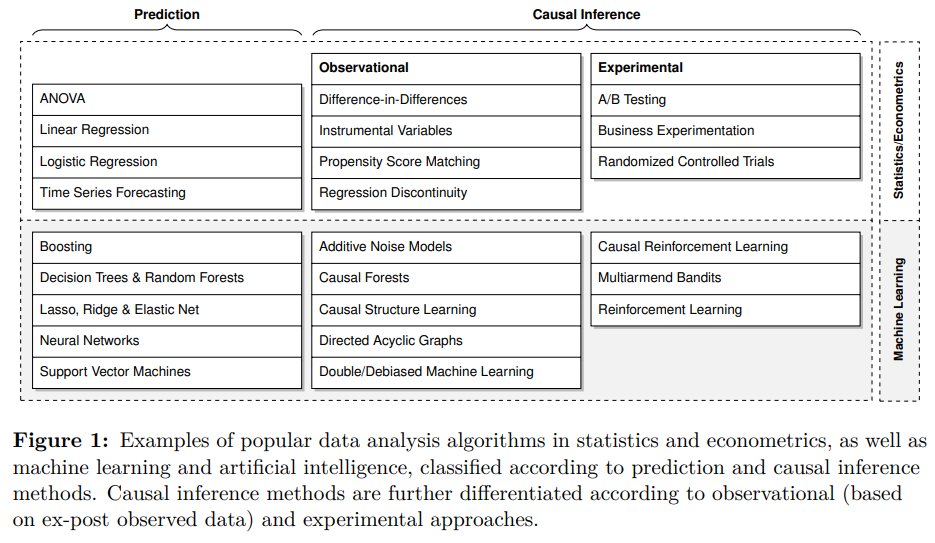
Fig 2. Prediction vs. Causal Inference Approaches, 벌꿀오소리의 공부 일지

전통적으로 인과추론은 통계 방법론적 접근이 일반적이었으나, 최근 ML 을 활용한 다양한 방법론이 제시되고 있다.
회사에서 보통 접하게 되는 A/B 테스팅이란 통계학 기반의 실험적 방법론이며, 이외에도 다양한 접근법이 존재.

Endogeneity (내생성)

문제 정의

변수 간 명확한 인과성을 파악하는데 가장 큰 방해요소는 내생성 (endogeneity) 이다.
내생성이란 독립 변수가 모델의 오차와 상관성을 가지는 경우를 의미한다.

$$ y_i = \alpha + \Beta x_i + \epsilon_i $$

아래와 같은 회귀식에서 유의미한 $\alpha$ 와 $\Beta$ 값을 얻기 위해선 다음 조건이 충족되어야 한다.

$$ E[{\epsilon}_i | x_i] = 0 $$

즉, $\alpha$ 와 $\Beta$ 로 설명되는 변수 $y_i$ 와 $x_i$ 간의 관계에서 설명되지 않는 다른 요인이 작용할 경우, 명확한 관계를 판별하는 것이 불가능해지는 것.
오차값에 의해 영향을 받는 변수 $x_i$ 는 내생변수 (endogenuous variable) 로 분류된다. 이와 다르게 모델 내 다른 어떤 값으로 부터도 영향을 받지 않는 변수는 외생변수 (exogenuous variable) 로 분류.

발생 원인

내생성의 주요 발생 원인은 다음과 같이 크게 세종류로 구분이 가능하다.

(1) Omitted Variables


Fig 3. Medium - Casual Inference with Linear Regression

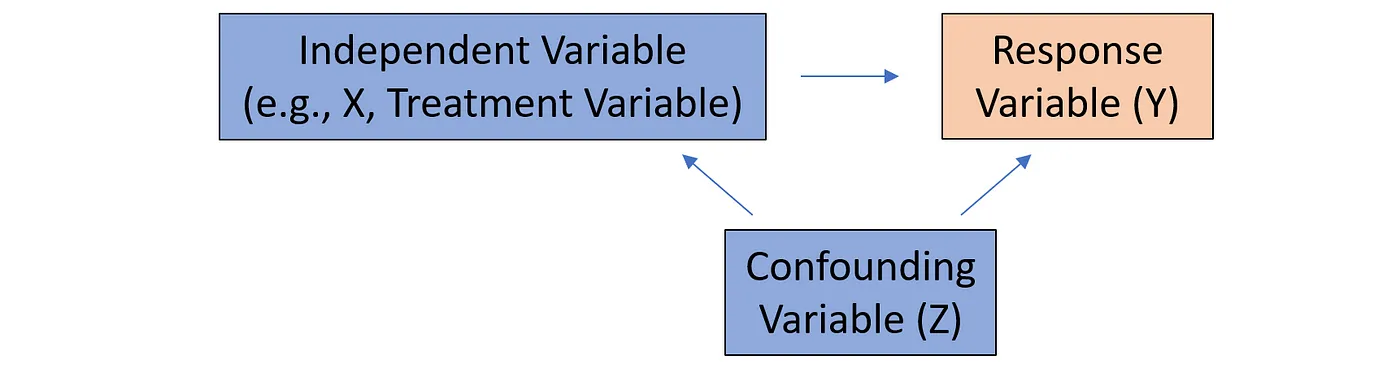
모델 내 존재하지 않는 변수 $Z$가 독립변수, 종속변수와 상관성을 가지게 될 경우 이를 교란변수 (Confounding Variable) 라 칭한다.
이러한 교란변수가 회귀식 내에 존재하지 않을 경우 (omitted), 이에 영향을 받는 독립변수는 오차값과 상관성을 가지기 때문에 내생변수가 되어버림.
회귀식에 교란변수를 더하면, 내생성이 사라지고 기존 독립변수의 상관계수가 올바른 값으로 수정됨.

(2) Simultaneity

내생성의 또 다른 원인은 종속변수가 독립변수에 영향을 미치는 경우이다. 이 경우 X -> Y 와 Y -> X 의 인과성이 모두 합당하기 때문에 실제 상관계수 산출에 어려움을 겪을 수 있다.
- 예) 높은 교육 수준이 평균 소득을 높이는 것은 사실이나, 평균 소득이 높은 가구는 교육에 더욱 많은 지출을 하는 것 또한 사실이다.
이러한 관계는 Simultaneity Bias 를 발생시키며, 관계에서 정확한 인과성을 파악하는 것이 불가능.

(3) Measurement Error

회귀식의 기본 전제는 모든 데이터가 정확하게 측정되었다는 것이나, 실제 측정 환경에서 오류가 발생했을 가능성이 있다.
이렇듯 오류가 발생한 측정값과 실제값 간의 차이를 측정 오차 (Measurement Error) 라고 칭한다.
종속변수 $Y$ 내 측정 오차가 존재하는 경우, 내생성이 발생하지 않는다. 반면 독립변수 $X$ 내 측정 오차가 존재하는 경우 내생성 발생.

Simpson’s Paradox

인과추론 과정에서 발생 가능한 대표적인 내생성 문제의 예시가 심슨의 역설 (Simpson’s Paradox) 이다.
간단히 설명해, 여러 그룹의 자료를 합했을 때의 결과가 각 그룹을 구분했을 때의 결과와 다른 때를 의미한다.
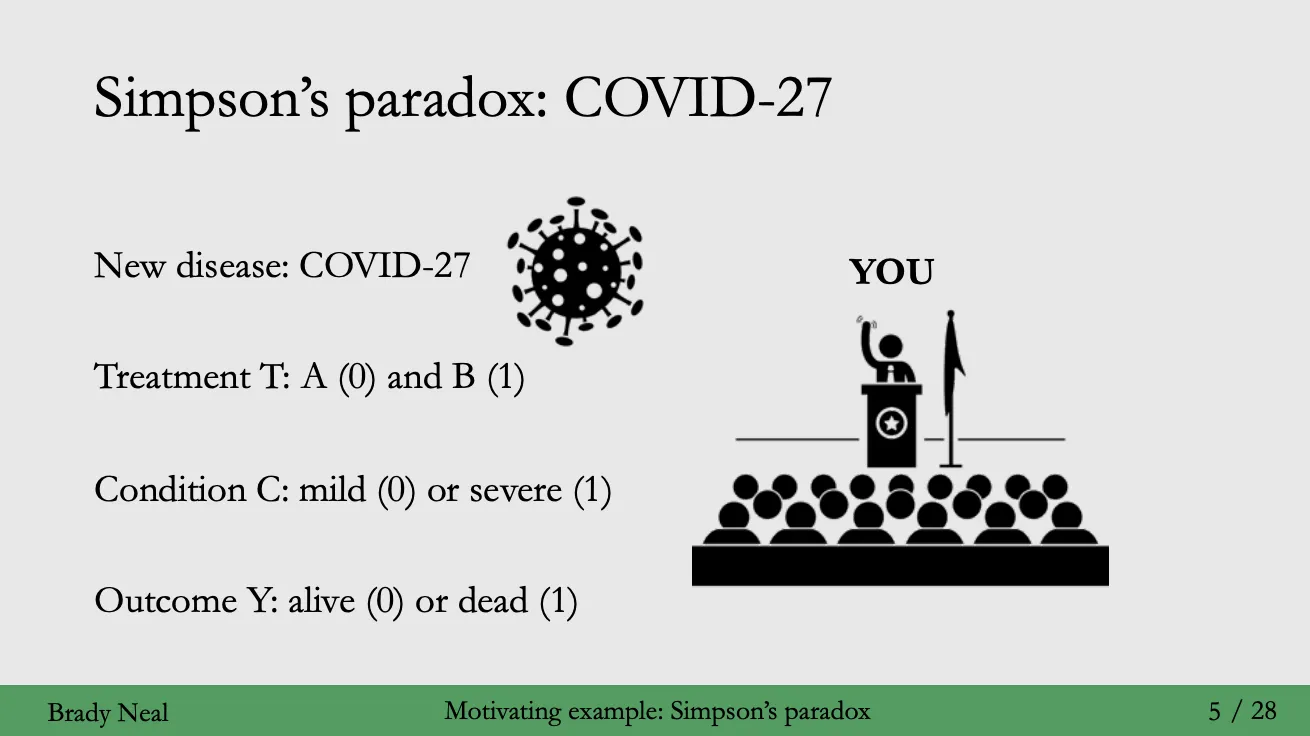
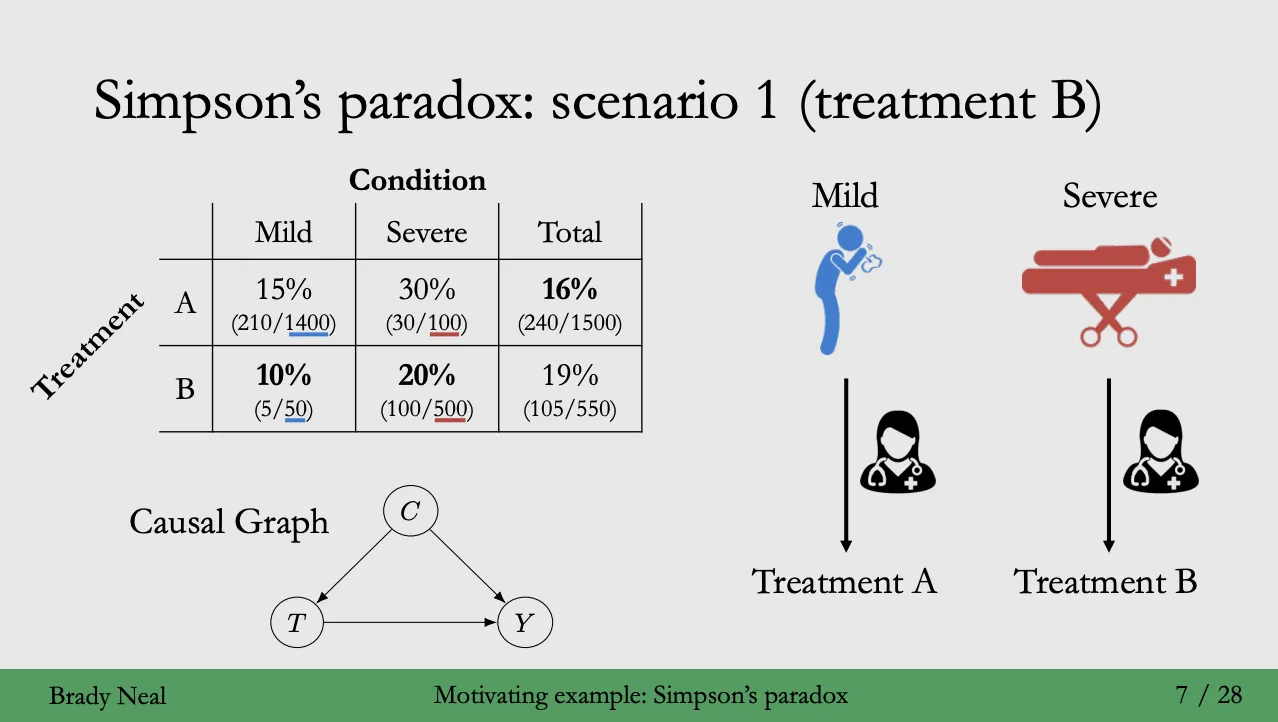
예시로 백신 A와 B 중 특정 질병을 치료하는데 더 나은 효과를 보이는 백신을 선택해야 한다고 가정해보자.


Fig 4. Medium - Simpson’s Paradox and Confounding

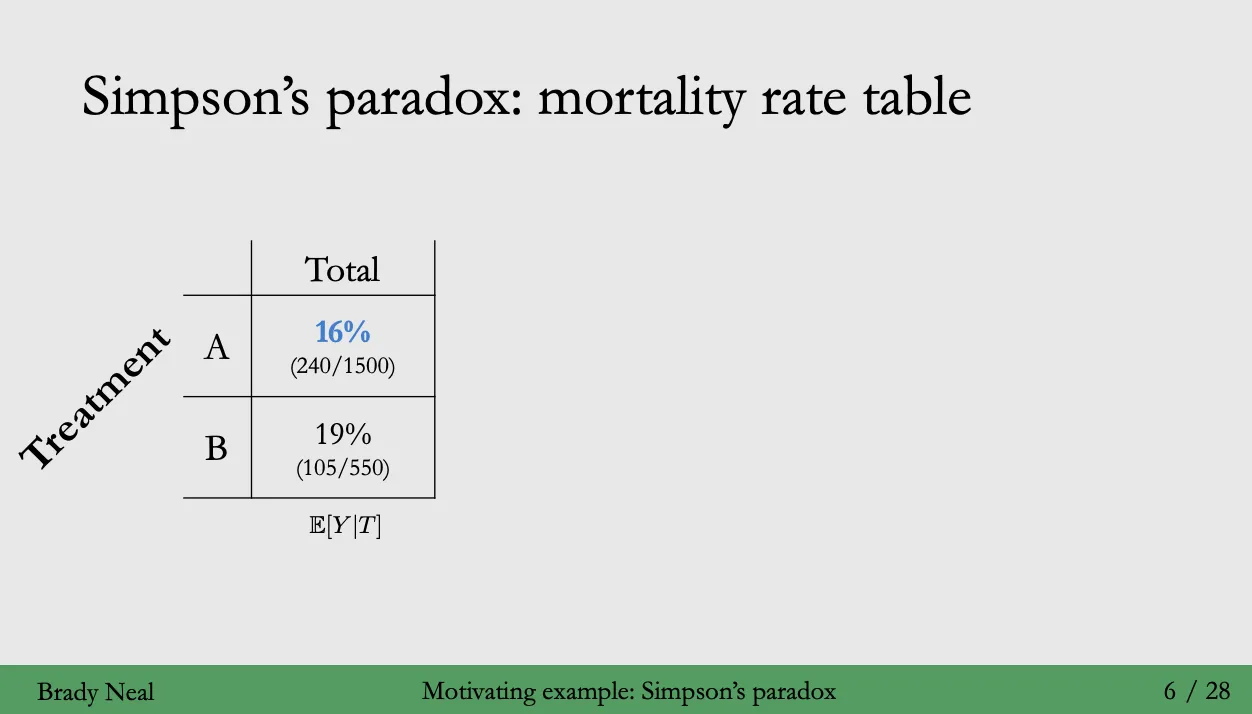
아래와 같이, 그룹을 단순하게 백신 A, B 를 맞았을 경우로 분리할 경우 다음과 같은 테이블을 얻을 수 있다.


Fig 5. Medium - Simpson’s Paradox and Confounding

당연히 상단의 수치만으로 비교하였을 경우, 사망률이 16% 로 더 낮은 백신 A를 선택하는 것이 타당하다.
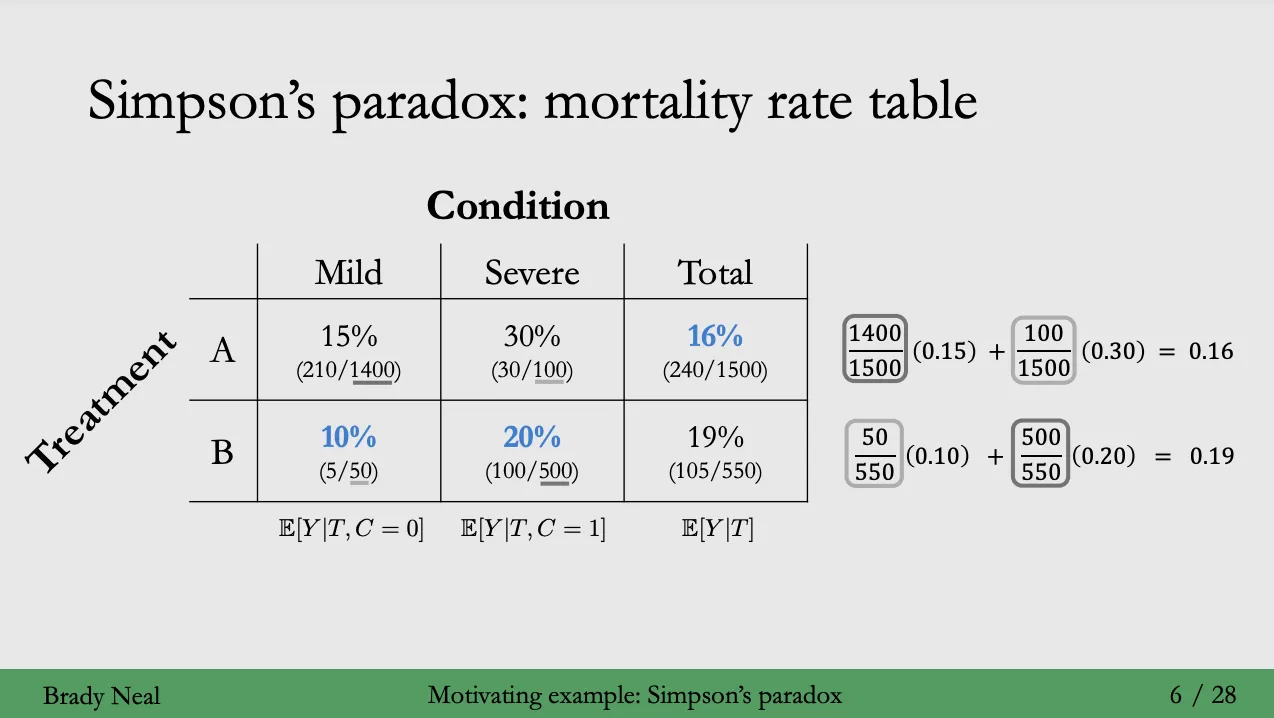
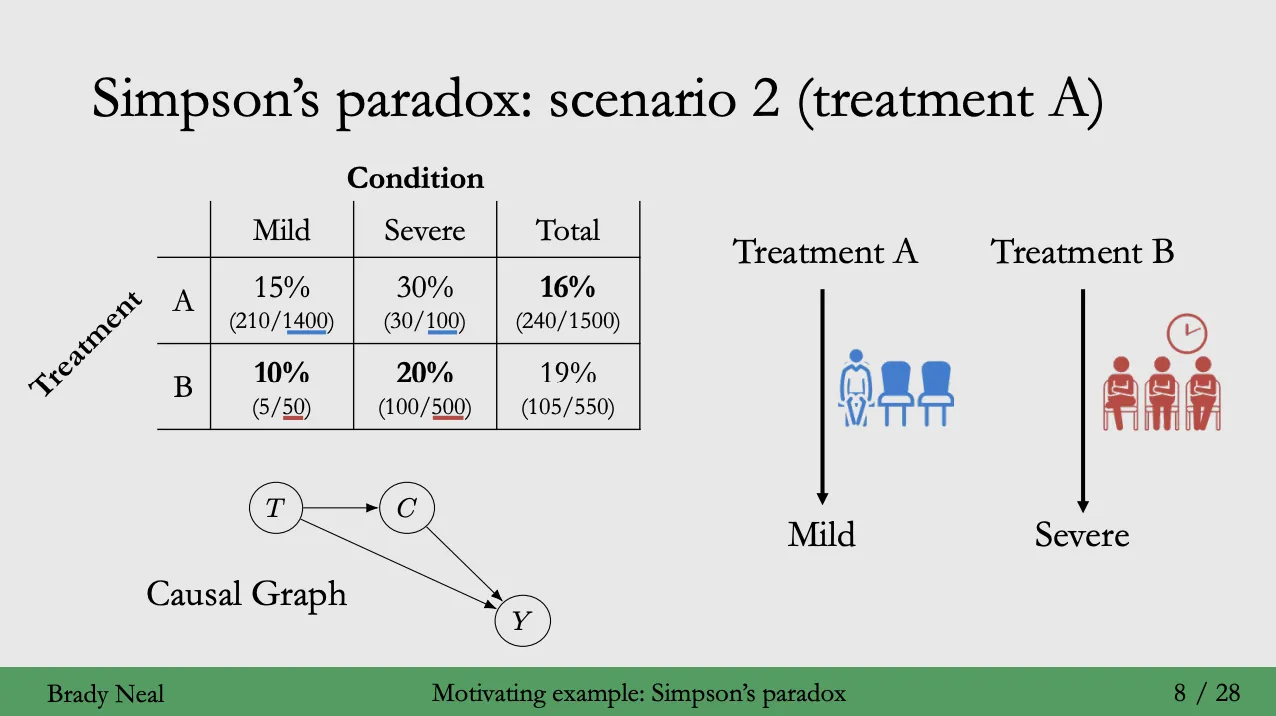
하지만 데이터를 세분화해, 환자가 백신을 맞기 전 상태로 나누어 확인하게되면 다음과 같이 반대의 결과값이 도출된다.


Fig 6. Medium - Simpson’s Paradox and Confounding

이와 같이 비직관적인 결과가 도출되는 이유는 Treatment A 를 처방받은 환자는 대부분 Mild 한 상태에 있었으며, Treatment B 를 처방받은 환자는 대부분 Severe 한 상태에 있었다는 점에 기인한다. 즉, 가중치에 차이가 존재.
이러한 상황에서 백신을 선택하기 위한 의사결정을 수행하기 위해서는, 문제의 인과 모형 (Causal Structure) 을 감안해야 한다.

Case A : 환자의 상태가 백신을 결정하는 경우


Fig 7. Medium - Simpson’s Paradox and Confounding

공급량의 차이로 인해 Treatment A 는 비교적 상태가 양호한 환자에게 투약하고, Treatment B 는 상태가 안좋은 환자에게 투약한 경우이다.
선별 방식의 차이로 다음과 같은 샘플 불균형이 발생한다.
- 백신 A를 투약 받은 그룹은 불균형적으로 사망할 확률이 낮은 환자가 다수를 구성.
- 백신 B를 투약 받은 그룹은 불균형적으로 사망할 확률이 높은 환자가 다수를 구성.
선별 방식이 구조적으로 불균형하기 때문에, 세분화된 분석결과를 참고하는 것이 타당하다 (백신 B 선정).
이 경우 내생성의 발생 원인은 백신 배분 방식이라는 교란변수이다.

Case B : 백신이 환자의 상태를 결정하는 경우


Fig 8. Medium - Simpson’s Paradox and Confounding

공급량의 차이로 인해 대기시간의 차이가 발생하였으며, 상대적으로 오래 기다린 Treatment B 환자의 상태가 더욱 악화된 경우이다.
- 백신 B를 투약 받은 그룹은 투약을 위해 대기하는 시간동안 사망할 확률이 높아지게 된다.
- 백신 A를 투약 받은 그룹은 투약을 위해 대기하는 시간이 없어 사망할 확률이 높아지지 않게 된다.
이러한 경우 선별 방식의 불균형성이 없고, 대기 시간 또한 Treatment 의 특성으로 볼 수 있기 때문에 합산된 분석결과를 참고하는 것이 타당하다 (백신 A 선정).
이 경우 인과관계의 복잡성은 증가했지만, 내생성이 발생했다고 볼 수 없다.

해결 방법


Fig 9. 벌꿀오소리의 공부 일지

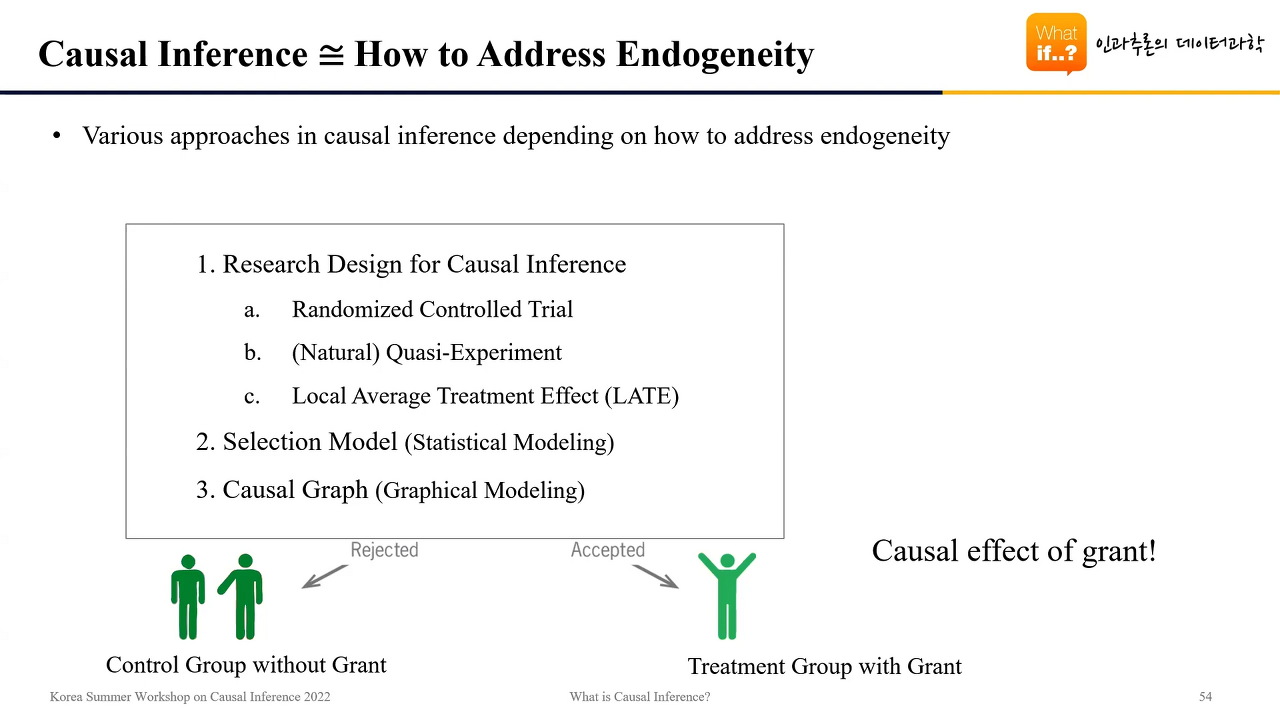
인과추론 과정에서 발생 가능한 내생성을 통제하기 위해 일반적으로 다음과 같은 3가지 방법을 사용할 수 있다.

Research Design
- Randomized Controlled Trial : 샘플 수집 과정을 디자인해 내생성을 통제하는 방식. 가장 효과적이지만 현실적인 한계가 존재한다.
- Quasi-Experiment : 실험과 관계 없이 발생한 데이터를 기반으로 실험 환경을 모방.
- Local Average Treatment Effect (LATE)
Selection Model
Causal Graph