소개
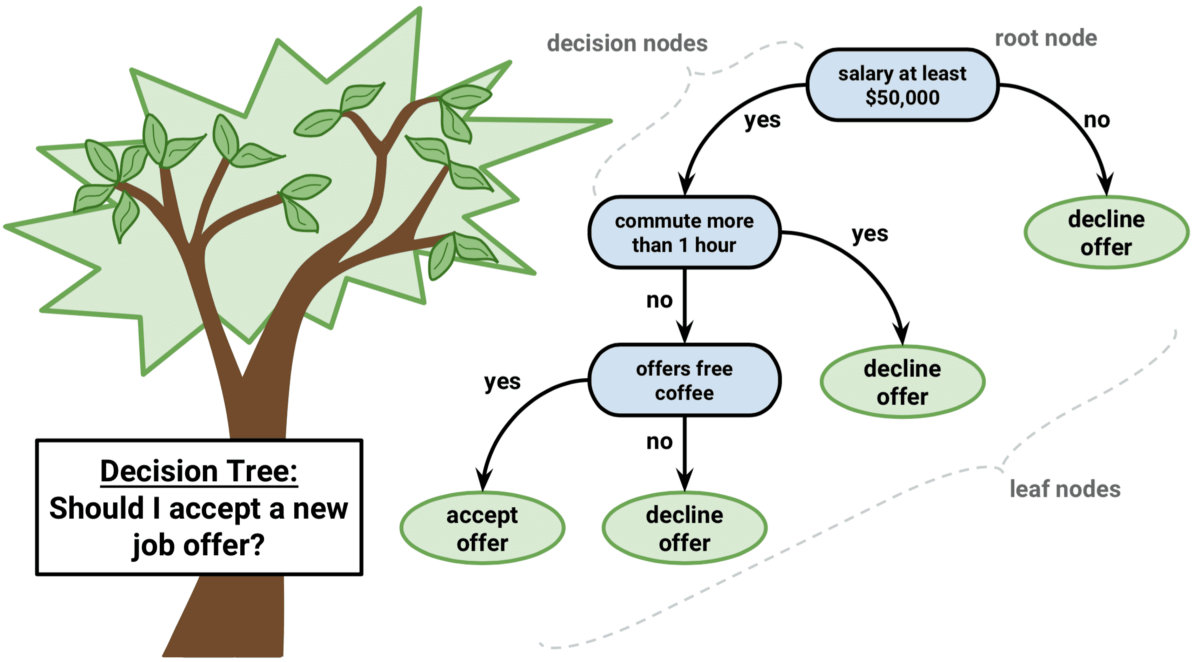
구직 활동 중 한 회사에서 입사제의를 받았다고 가정하자. 개인마다 그 정도에는 차이가 있겠지만, 제안을 수락하기 까지에는 일종의 의사결정 체계가 존재할 것이다. 대표적으로 다음과 같은 질문을 자신에게 던져볼 수 있다.
- 나의 배경과 직급에 적당한 보수를 받을 수 있는가?
- 출근 위치는 내가 감내할 수 있는 거리 내에 있는가?
- 직원 복지제도가 존재하는가?
질문에 연관성이 있는 데이터를 가지고 있다면 (보수, 통근거리, 복지제도 유무), 다수의 입사제의에 대해 수락(1) 또는 거절(0) 중 하나의 클래스로 제안에 대한 답변을 분류할 수 있는 알고리즘을 만들 수 있다. 이와 같이 일련의 결정 체계를 통해 분류와 회귀 문제를 효율적으로 수행하는 머신러닝 알고리즘을 결정 트리라고 부른다.
버클리와 스탠포드에서 1977년 개발한 CART 알고리즘 (Breiman et al.) 을 그 기반으로 하고있으며, 2010년 후반부터 널리 사용되고있는 LightGBM, XGBoost 와 같은 앙상블 학습 알고리즘의 기반이기도하다.
결정 트리
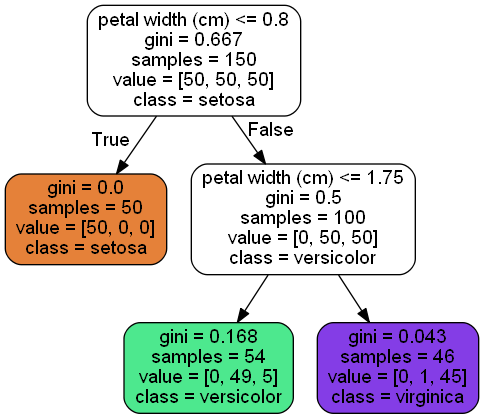
머신러닝 예시에서 자주 사용되는 Iris 데이터셋을 활용해 모델의 작동방법을 자세히 알아보자. 아래 시각화된 모델은 주어진 붓꽃의 꽃잎 길이를 기반으로 품종을 분류한다. 먼저 첫 노드에서는 꽃잎의 길이 (petal width) 가 0.8 cm 보다 작거나 같은지 확인한 다음, 그렇다면 붓꽃의 품좀을 setosa 클래스로 분류한다.
만약 꽃잎의 길이가 0.8 cm 보다 클 경우, 모델은 다음 노드로 이동하여 꽃잎 길이가 1.75 cm 보다 작거나 같은지 확인한다. 그렇다면 붓꽃을 versicolor 클래스로, 그렇지 않다면 virginica 클래스로 분류한다.
 |
|---|
| Fig 1. Sklearn 패키지의 결정 트리 모델 예시 |
노드의 samples 속성은 학습 과정에서 얼마나 많은 훈련 샘플이 적용되었는지를 헤아리고 있다. 예를 들어 위 예시의 경우 총 150 개의 데이터를 기반으로 학습되었으며, setosa 클래스에는 50 개의 데이터가, versicolor 클래스에는 54 개의 데이터가 학습 과정에서 사용되었던 것을 확인할 수 있다.
이에 반해 value 속성은 노드에 속한 각 클래스 별 데이터의 수를 보여준다. 예를 들어 우측 하단의 virginica 클래스에는 setosa 클래스가 0 개, versicolor 클래스가 1 개, virginica 클래스가 45 개가 분류되었다. 분류 체계가 완벽하지 않음을 뜻하며, 이는 gini 속성, 즉 이후 설명할 지니 불순도와 연계된다.
지니 불순도와 엔트로피
지니 불순도 (Gini Impurity Score)
지니 불순도는 특정 노드에 얼마나 다양한 클래스가 분포해있는지를 측정하는 성능 지표이다. 노드에 속해있는 샘플의 클래스 분포가 작을수록 0 에 가까워지며, $p_{i,k}$ 를 $i$ 번째 노드에 속한 샘플 중 클래스 $k$ 에 속한 샘플의 비율이라고 했을때 노드 $i$ 에 대한 지니 불순도 $G_i$ 는 다음과 같이 정의할 수 있다.
$$ G_i = 1 - \sum_{k=1}^n p_{i,k}^2 $$
엔트로피 (Entropy)
지니 불순도와 interchangeably 사용되는 개념이며, 본래 열역학의 개념이다 (분자가 안정되고 질서 정연할 수록 엔트로피는 0에 가까워진다). 노드 $i$ 에 대한 엔트로피 $H_i$ 는 다음과 같이 정의된다.
$$ H_i = - \sum_{k=1, p_{i,k} \neq 0}^n p_{i,k} \cdot log_2(p_{i,k}) $$
지니 불순도와 엔트로피 간 생성하는 모델에 큰 차이는 없으며, 지니 불순도의 연산속도가 더 빠르기 때문에 일반적으로 트리 기반 모델은 지니 불순도 평가 지표를 사용하고있다. 다만 모델에 차이가 발생하는 경우 엔트로피가 상대적으로 더 균형 잡힌 트리를 만들게된다.
여기서 드는 의문점은 지니 불순도와 엔트로피 모두 개별적인 노드에 대한 성능 지표라는 점이다. 일반적인 기계학습이란 모델의 단일 성능 지표 (RMSE, Cross Entropy 등) 를 기반으로 오차율을 줄이는 과정을 거치게 되는데, 결정 트리는 학습 과정 시 전체 모델이 아닌 개별 노드의 성능만을 최적화한다. 이러한 알고리즘을 Greedy Algorithm 이라 칭한다.
CART 훈련 알고리즘
CART (Classification And Regression Tree) 는 데이터에 대한 최적의 의사 결정 기준을 찾기 위해 고안된 알고리즘이다. 개념적으로 CART 알고리즘은 다음과 같은 순서로 수행된다.
- 훈련 세트를 여러 특성 $k$ 와 임곗값 $t_k$ 의 조합으로 반복해 분리한다 (예. 꽃잎의 길이 <= 2.45 cm).
- 매 사이클 마다 나누어진 두 서브셋에 대한 다음 비용 함수를 계산한다. (여기서 $G$ 는 서브셋의 불순도, $m$ 은 서브셋의 샘플 수를 뜻한다)
$$ J(k, t_k) = \frac{m_{left}}{m} G_{left} + \frac{m_{right}}{m} G_{right} $$
- 가장 작은 비용 함수를 가진 특성과 임곗값 조합으로 데이터를 나눈다.
- 요건을 충족할때 까지 동일한 방식을 통해 나누어진 서브셋에 대한 최적의 특성과 임곗값 조합을 찾는다.
설명한바와 같이 CART 알고리즘은 Greedy Algorithm (탐욕적 알고리즘) 이다. 매 단계에서 알고리즘은 주어진 노드에 대한 최적의 특성과 임곗값 조합을 찾을뿐, 그 이후 과정에 대한 고려는 하지 않는다.
하이퍼파라미터
결정 트리는 별다른 데이터 전처리를 필요로하지 않을뿐만 아니라, 별다른 하이퍼파라미터 또한 필요로 하지 않는다. 대표적으로 조절할 수 있는 것은 결정 트리의 깊이 (depth) 인데, 이는 트리의 높이에 해당하는 개념이며 Scikit-learn 패키지는 max_depth 매개변수를 통해 이를 조절한다. max_depth 의 값이 낮을수록 모델을 규제하는 효과를 가진다. 이외에 Scikit-learn 패키지 DecisionTreeClassifier 가 가진 매개변수는 다음과 같다.
min_samples_split: 분할되기 위해 노드가 가져야 하는 최소 샘플 수min_samples_leaf: 리프 노드가 가지고 있어야 할 최소 샘플 수max_leaf_nodes: 리프 노드의 최대 수max_features: 각 노드에서 분할에 사용할 특성의 최대 수
회귀 문제 적용
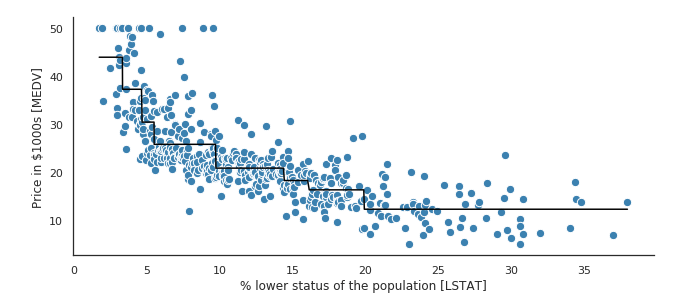
클래스의 개념에 노드에 속한 샘플의 평균값을 대입하면 결정 트리를 회귀 문제에 또한 적용할 수 있다. 다만 여기서 CART 알고리즘은 훈련 세트를 불순도를 최소화하는 방향으로 분할하는 대신 평균제곱오차 (MSE) 를 최소화하도록 분할하도록 작동한다.
$$ J(k,t_k) = \frac{m_{left}}{m} MSE_{left} + \frac{m_{right}}{m} MSE_{right} $$
 |
|---|
| Fig 2. 결정 트리를 사용한 회귀 모델 예시 |
참고 자료
- Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow
- https://www.explorium.ai/blog/the-complete-guide-to-decision-trees/