Introduction

• 모델의 과대적합 (Overfitting) 을 방지하는 대표적인 기법으로 모델 규제 방법이 있다.
• 회귀 모델의 경우 보통 모델 가중치를 제한하는 방법을 통해 규제를 가하는데, 이를 정규화 (regularization) 라 칭한다. 모델 가중치에 제한을 두는 방법론은 비단 회귀 모델 뿐 아니라 딥러닝 영역에도 적용된다 - 참고 글.
• 본 글에서는 대표적인 회귀 모델의 가중치 적용법인 Ridge, Lasso Regression 과 이 두 방법론을 복합적으로 활용하는 엘락스틱넷을 소개한다.

Regression Analysis

Fig 1. Jason Wong - Linear Regression

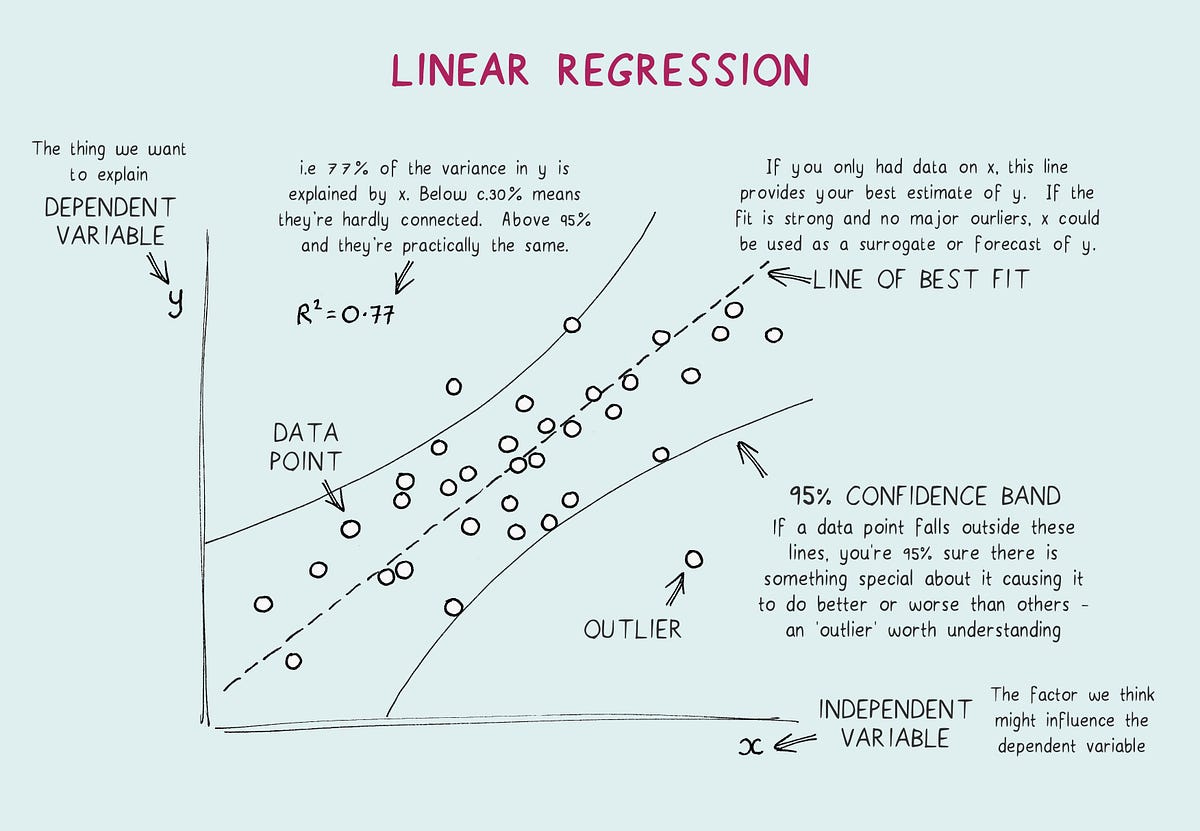
• 통계적 예측 분석의 기본이 되는 회귀 분석이란, 독립변수 $x$ 에 대응하는 종속변수 $y$ 와 가장 비슷한 값 $\hat{y}$ 을 출력하는 함수 $f(x)$ 를 찾는 과정을 의미한다.

Linear Regression (선형회귀식)

$$ \hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + … + \theta_D x_D $$

• 만약 $f(x)$ 가 위와 같은 선형함수인 경우 해당 함수를 선형회귀모형 (Linear Regression Model) 이라 칭한다.
• 위 식에서 독립변수 $x = (x_1, x_2, … , x_D)$ 는 D차원의 벡터이며, 가중치 벡터 $w = (w_0, … , w_D)$ 는 함수 $f(x)$ 의 계수 (coefficient) 이자 회귀 모형의 모수 (parameter) 라고 부르게된다.

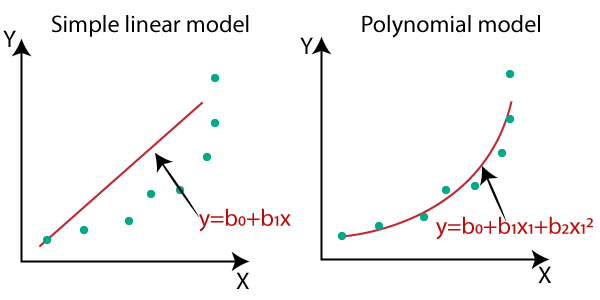
Polynomial Regression (다항회귀식)

Fig 2. Java Point - ML Polynomial Regression

• 독립변수와 종속변수가 비선형 연관성을 가질 경우, 독립변수의 차수를 높여 다항식 함수를 활용할 수 있으며 이를 다항회귀식이라 부른다.

$$ \hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1^2 + \theta_4 x_2^2 + \theta_5 x_1x_2 $$

• 한 개 이상의 독립변수가 존재할 경우 변수 간 영향을 파악하는 것이 가능하다 (예. $x_1x_2$).
• 차수가 지나치게 높을 경우 과적합이 발생할 위험이 상승한다. 이러한 경우 Cross Validation 을 통해 적합한 차수 선정이 가능.

The Normal Equation (정규방정식)

• 그렇다면 최적의 선형회귀식은 어떻게 계산할 수 있을까?
• 데이터가 주어졌을때 최적의 추세선을 그리기위한 대표적인 방법 중 하나는 최소제곱법 (Ordinary Least Square, OLS) 이다.
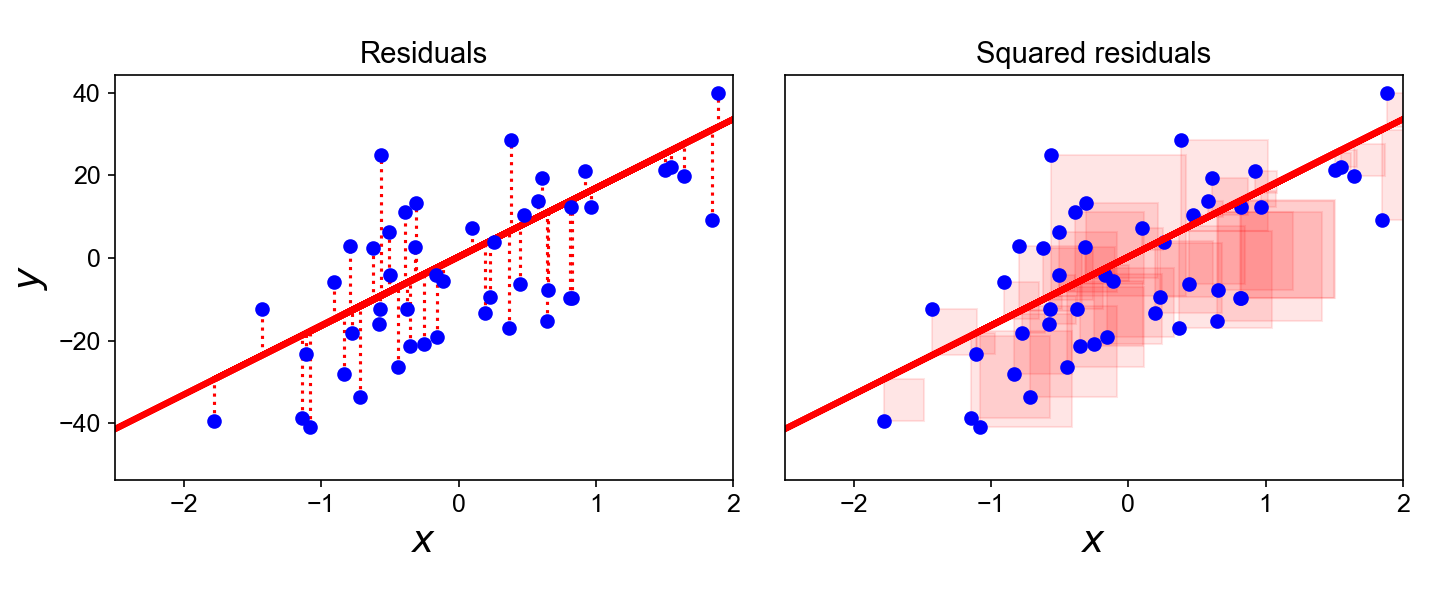
• 최소제곱법은 실제 데이터 $y$ 와 추세선의 예측값 $\hat{y}$ 간 차이 (잔차, Residual) 의 제곱합을 최소화하는 추세선을 찾는 방법이다. 아래 그림 참고.

Fig 3. Gregory Gunderson - Ordinary Least Squares

• 잔차의 제곱합을 최소화하는 선형함수의 계수는 다음과 같은 행렬연산을 통해 계산이 가능하며, 해당식을 정규방정식이라 부른다.

$$ \hat{\theta} = (X^T X)^{-1} X^T y $$

• 주의할 점은 OLS 는 선형회귀모델의 추정 방법 중 하나일 뿐, 선형회귀모델 자체는 아니라는 점이다. 선형회귀문제 해결을 위해 경사하강법 활용 또한 가능하다.
• 하지만 OLS 방법론은 경사하강법 과는 달리 한번의 연산으로 최적 계수 산정이 가능하다.
• 무려 1800년대 초 Gaussian Distribution 의 그 가우스가 해당 기법을 활용해 소행성 세레스의 궤도를 예측하며 알려지게 되었다 - 출처.

Ridge (L2) Regression

• Ridge Regression 은 통계학에서 능형회귀, 또는 Tikhonov Regularization 이라고 불리며, 다음과 같은 비용함수를 활용해 회귀식을 추정한다.

$$ J(\theta) = MSE(\theta) + \alpha \frac{1}{2} \sum_{i=1}^{n} \theta_i^2 $$

• 뒷단의 정규화식 $\alpha \frac{1}{2} \sum_{i=1}^{n} \theta_i^2$ 은 모델 학습과정에서만 감안될 뿐, 실제 예측 과정에서 제외되어야 한다.
• Ridge Regression 이 적용된 선형 함수는 데이터에 대한 잔차뿐 아니라 계수값 또한 최소화하게 되며, 이는 종속변수 예측에 비핵심적인 계수값을 줄이는 효과를 가진다.
• 하이퍼파라미터 $\alpha$ 를 통해 규제량을 통제할 수 있으며, 이를 매우 큰 값으로 설정할 경우 모든 계수값에 0 에 근접해지는 효과를 가진다.
• Ridge Regression 수행을 위한 정규방정식은 다음과 같다 ($A$ 는 (n+1) x (n+1) 크기의 Identity Matrix 이며, 가장 왼쪽 상단의 값이 $0$ 이다).

$$ \hat{\theta} = (X^T X + \alpha A)^{-1} X^T y $$

Lasso (L1) Regression

• Lasso (Least Absolute Shrinkage and Selection Operator) Regression 은 기본적으로 Ridge Regression 과 동일하지만 계수의 제곱값이 아닌 절대값을 활용한다.

$$ J(\theta) = MSE(\theta) + \alpha \sum_{i=1}^{n} |\theta_i| $$

• Lasso Regression 의 가장 중요한 성질은 종속변수 예측에 비핵심적인 변수를 모델에서 제외하는 효과를 가진다는 점이다. 이는 해당 변수의 계수를 낮게 산정하지만, 제외하지는 않는 Ridge Regression 과 차이를 가진다.
• 상기된 효과는 일종의 Feature Selection 과정으로 해석하는 것이 가능하다.
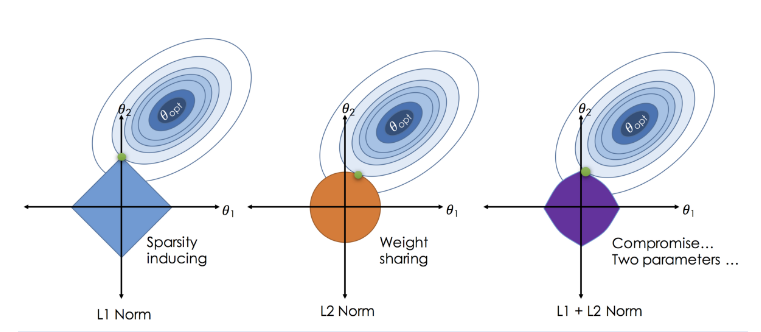
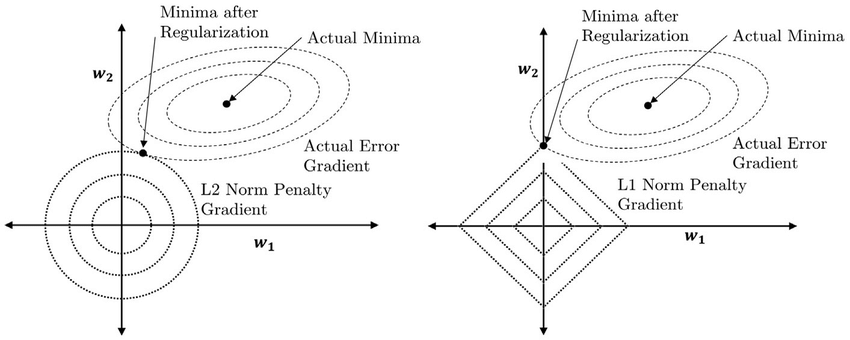
• 이러한 효과가 나타나는 이유는 L1 Norm (절대값) 은 크기에 관계없이 모든 계수를 동일하게 취급하는 반면, L2 Norm (제곱값) 은 크기가 큰 계수에 더욱 큰 가중치를 부여하기 때문이다. 따라서 최적화 시 계수의 감소 속도에 차이를 가지게 된다.

Fig 4. Research Gate - L1 vs. L2 Norm

• 위 그림은 L1 vs. L2 정규화 함수가 동일한 손실값을 산정하는 영역을 나타낸다. 제곱값은 원형으로, 절대값은 사각형으로 묘사되는 것을 확인할 수 있다.

Elastic Net

• 엘라스틱넷은 Ridge Regression 과 Lasso Regression 을 복합적으로 활용하는 정규화 기법이다.

$$ J(\theta) = MSE(\theta) + r\alpha \sum_{i=1}^{n} |\theta_i| + \frac{1-r}{2}\alpha \sum_{i=1}^{n} \theta_i^2 $$

• 하이퍼파라미터 $r$ 을 활용하여 각 기법의 영향도를 조절할 수 있으며, 한가지 기법만을 활용하는 것 또한 가능하다.
• 일반적인 회귀 문제에선 정규화를 반드시 포함하는 것이 권장된다. Ridge Regression 은 좋은 시작 지점이나, feature 선별이 필요한 경우 Lasso 또는 엘라스틱넷을 활용하는 편이 좋다.
• Lasso Regression 은 feature 수가 지나치게 많거나 multicollinearity 가 존재하는 경우 이상행동을 보일 수 있으며, 엘라스틱넷의 경우 이러한 문제가 덜한 편.

Sources

1. O’Reilly - Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow
2. StatQuest - Regularization with Regression [1][2][3]
3. Handson ML - 릿지, 라쏘, 엘라스틱 넷
4. 데이터 사이언스 스쿨 - 선형회귀분석의 기초