모델링을 위한 특성 선별 방법 (Feature Selection)

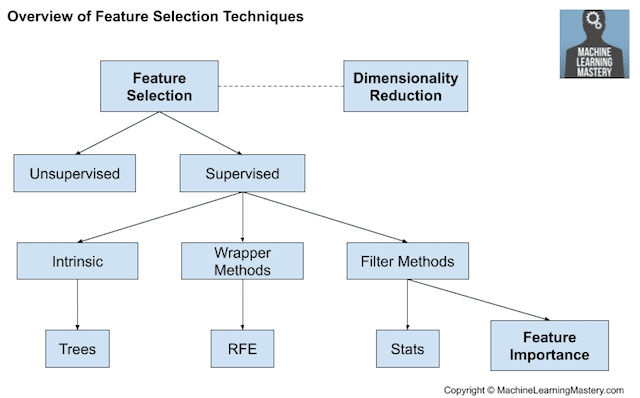
Introduction

운영되는 서비스에서 파생되는 데이터의 종류는 매우 다양하고, 이 중 모델링에 유용한 데이터를 추려내 활용하는 변수 선별 과정은 어렵지만 필수적인 일이다. 정돈된 방식으로, 유의미한 데이터를 선별해 모델링을 진행하지 않을 경우 발생할 수 있는 문제점은 다음과 같이 정리할 수 있다.

지나친 노이즈로 인해 오버피팅이 발생할 수 있다.
모델 성능이 저하될 수 있다.
불필요한 학습 시간이 발생할 수 있다.

실무적인 feature selection 과정에선 문제 환경에 기반한 적절한 가설 설정과 테크니컬한 검증 과정이 병행되어야 한다. 아무리 feature 의 유용성이 수치화된다고 하더라도, 조직이 보유하고 있는 모든 데이터를 활용하는 것은 불가능하기 때문이다.

다음 글은 비즈니스 적인 가설 설정보다는, 이를 검증하기 위한 테크니컬 방법론을 크게 Filtering, Wrapping, Embedding 세 분류로 정리한다.

Filter 기반 방법

변수 간 관계성에 기반해 모델 활용에 유용한 feature 를 선정하는 방식이다. 선택 과정에서 실제 모델링을 진행하지는 않으며, 연산처리가 빠른 대신 실제 모델 적용 시 예기치 못한 결과가 발생할 수 있다는 단점을 가진다. 특성상 통계적 방법론이 주를 이룬다.

alt text

Mutual Information

정보이론에서 두 개 변수에 대한 Mutual information 이란, 하나의 변수를 통해 다른 변수에 대해 얻을 수 있는 정보의 양을 설명하며, 보편적인 Correlation Coefficient 와 달리 변수 간 선형관계나, 연속성을 요하지 않는다.

$$ \text{Mutual Information} = \sum_{x\in X}\sum_{y\in Y} p(x,y) \text{log}[\frac{p(x,y)}{p(x)p(y)}] $$

위 방정식에서 $p(x,y)$ 는 $x, y$ 변수의 결합확률을, $p(x)$ 와 $p(y)$ 는 각각 $x, y$ 변수의 주변확률을 의미한다. 두 변수 중 하나의 값이 변동하지 않는 경우 Mutual Information 은 $0$ 에 근접한 값을 가지며, 변수 간 정보성이 커질수록 (예. 두 변수가 항상 같은 값을 가지는 경우) Mutual Information 은 큰 값을 가지게 된다.

변수값이 연속성을 가지는 경우, binning 을 통한 카테고리화가 필요하다. 즉, Mutual Information 은 카테고리 변수 활용을 위한 Feature Selection 방법론으로 생각할 수 있다.

1
2
3
4
5
6
7


from  sklearn.feature_selection import mutual_info_classif
import matplotlib.pyplot as plt

importances = mutual_info_classif(X, Y)
feat_importances = pd.Series(importances, dataframe.columns[0:len(dataframe.columns)-1])
feat_importances.plot(kind='barh', color='teal')
plt.show()

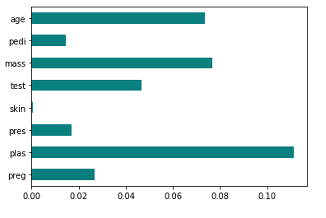
alt text

Chi-square Test

카이제곱검정이란 특정 변수에 대해 가설적으로 설정한 분포와 실제 관측된 분포 간 차이에 대해 통계적 유의성을 구하는 과정을 뜻한다 (예. 동전을 100번 던졌을때 해당 동전이 fair coin 인지 검증).

데이터가 주어졌을때 분석가는 인풋 변수와 타겟 변수가 독립적이라는 가설 하에 다음 방정식을 활용해 인풋 변수의 모든 값에 대한 expected frequency 를 구할 수 있다.

$$ P(AB) = P(A) \cdot P(B) $$

하지만 이렇게 도출된 값은 실제 데이터를 가공해 구한 $P(AB)$ 와 차이를 가질 것이다. 이렇게 구한 expected frequency 와 실제 관측된 frequency 간 차이가 클때, 해당 변수는 타겟 변수에 대해 높은 종속성을 가지며, 유용한 feature 라고 판단할 수 있게 되는 것.

(분포를 직접 비교하는 것이 아니다. 변수 간 독립성 가설이 기각되는지 여부에 따라 종속성을 판단하는 과정이라고 생각하는 것이 보다 정확하다)

$$ \Chi_c^2 = \sum \frac{(O_i - E_i)^2}{E_i} $$

위 방정식에서 $O_i$ 은 observed value, $E_i$ 은 expected value 를 의미한다.

카이제곱검정 활용에는 다음과 같은 제약 사항이 존재한다.

모든 변수가 카테고리 변수일 것
독립적으로 샘플링 되었을 것
모든 값에 대한 expected frequency 가 5 이상일 것

1
2
3
4
5
6
7
8
9


from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

#convert to categorical data by converting data to integers
X_cat = X.astype(int)

#three features with highest chi-squared stats selected
chi2_features = SelectKBest(chi2, k=3)
X_kbest_features = chi2_features.fit_transform(X_cat, Y)

Fisher’s Score

전통적인 Feature Extraction 방법론이다. ANOVA 와 유사하게 타겟 카테고리 별 분산과, 전체 데이터의 분산을 비교해 통계치를 산출하는 방법 - 참고 글. 산정된 통계치를 나열해 가장 “유의미한” feature 를 특정하는 것이 가능하다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


from skfeature.function.similarity_based import fisher_score
import matplotlib.pyplot as plt

#calculating scores
ranks = fisher_score.fisher_score(X, Y)

#plotting ranks
feat_importances = pd.Series(importances, dataframe.columns[0:len(dataframe.columns)-1])
feat_importances.plot(kind='barh', color='teal')
plt.show()

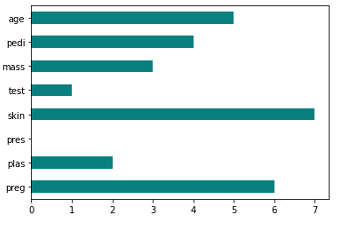
alt text

Correlation Coefficient

변수 간 선형 관계를 측정해 상관성이 높은 feature 를 추리는 방법이다. 타겟 변수와의 상관성을 파악하는 것은 물론, feature 간 상관성 또한 파악할 수 있기 때문에 다중공신성 문제를 사전에 인지하는데에 도움을 줄 수 있다.

하지만 해당 방법론 또한 분명한 단점들이 존재한다. 대표적으로 비선형 관계성을 파악하지 못한다는 점을 들 수 있는데, 실무적 환경에서 구축하는 모델이 대부분 비선형성 관계를 전제한다는 점을 생각했을때 실제 모델 적용에 부적합한 방법일 가능성이 높다.

(다만 $R^2$ 와 같은 결정계수를 활용한다면 실제 선형 관계를 가지는 feature 를 특정하는데 도움을 줄 수 있다)

또 다른 단점은 선형관계 파악에 지표의 연속성이 전제된다는 점이다. 따라서 타겟 변수가 카테고리 변수인 경우, 상관성을 활용한 특성 선별은 다소 부적합할 수 있다. 문제 특성과 변수의 종류에 따라 여러 방법을 혼용해서 사용하는 것이 필요할 수 있고, 이렇듯 여러가지 접근법으로 동일한 변수가 반복적으로 선별되는 경우 해당 변수는 모델 성능에 기여할 확률이 높을 것이다.

1
2
3
4
5
6
7
8
9


import seaborn as sns
import matplotlib.pyplot as plt

#correlation matrix
cor = dataframe.corr()

#plotting heatmap
plt.figure(figsize = (10,6))
sns.heatmap(cor, annot = True)

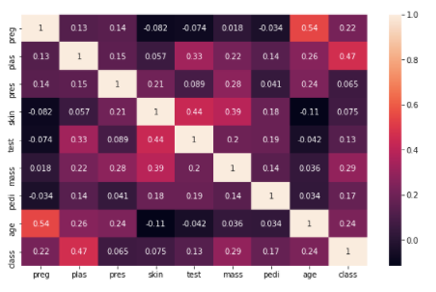
alt text

Wrapper 기반 방법

실제 데이터의 subset 을 활용해 모델링을 진행하고, 성능 지표에 기반해 가장 높은 성능을 보이는 feature 집합을 특정하는 방식이다. 당연한 이야기이지만, 모델 적용 환경에서 검증된 feature set 을 특정할 수 있는 대신 연산속도가 느리다는 단점을 가진다.

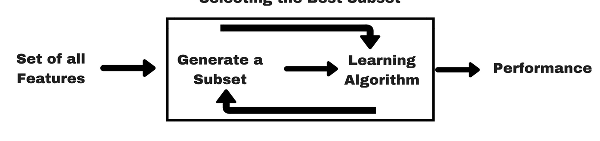
alt text

Forward Feature Selection

성능 기여도가 가장 높은 feature 를 시작으로, feature set 을 순차적으로 늘려가는 방식이다. 마치 greedy algorithm 과 같이 주어진 단계에서, 개별 변수의 기여도를 기반으로 의사결정을 내리는 만큼 변수 조합의 시너지 효과가 충분히 반영되지 않을 수 있다.

또한 모델 정의가 선행되기 때문에 파라미터 튜닝과 병렬로 진행될 경우 많은 자원이 소모될 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


from mlxtend.feature_selection import SequentialFeatureSelector
from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(class_weight='balanced', solver='lbfgs', n_jobs=-1, max_iter=500)
lr.fit(X, Y)

ffs = SequentialFeatureSelector(lr, k_features='best', forward=True, n_jobs=-1)
ffs.fit(X, Y)

features = list(ffs.k_feature_names_)
features = list(map(int, features))

lr.fit(x_train[features], y_train)
y_pred = lr.predict(x_train[features])

Backward Feature Elimination

모든 feature set 을 대상으로 모델링을 진행한 후, 순차적으로 기여도가 낮은 feature 를 제외하는 방식이다. 기본적으로 forward feature selection 과 유사한 장단점을 가진다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


from mlxtend.feature_selection import SequentialFeatureSelector
from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(class_weight='balanced', solver='lbfgs', n_jobs=-1, max_iter=500)
lr.fit(X, Y)

ffs = SequentialFeatureSelector(lr, k_features='best', forward=False, n_jobs=-1)
ffs.fit(X, Y)

features = list(ffs.k_feature_names_)
features = list(map(int, features))

lr.fit(x_train[features], y_train)
y_pred = lr.predict(x_train[features])

Exhuastive Feature Selection

가능한 모든 feature 조합을 비교해 가장 성능이 좋은 feature set 을 추리는 방식이며, 관점에 따라 가장 신뢰도가 높은 방법일 수 있으나 연산 과정에 비효율적인 측면이 존재한다. 데이터 규모에 따라 많은 자원이 소모될 수 있기때문에 문제 적용에 적합한지에 대한 충분한 고민이 필요하다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


from mlxtend.feature_selection import ExhaustiveFeatureSelector
from sklearn.ensemble import RandomForestClassifier

#create the ExhaustiveFeatureSelector object
efs = ExhaustiveFeatureSelector(
    RandomForestClassifier(),
    min_features=4,
    max_features=8,
    scoring='roc_auc',
    cv=2
)

#fit the object to the training data
efs = efs.fit(X, Y)

#print the selected features
selected_features = x_train.columns[list(efs.best_idx_)]
print(selected_features)

Recursive Feature Elimination

우선 전체 feature set 을 대상으로 모델링을 진행한 후, correlation coefficient 와 같은 특정한 지표를 기반으로 일정 비중의 feature 를 제외하는 방법을 재귀적으로 반복하게 된다.

1
2
3
4


from sklearn.feature_selection import RFE
rfe = RFE(lr, n_features_to_select=7)
rfe.fit(x_train, y_train)
y_pred = rfe.predict(x_train)

Embedded 방법

모델 구조 내 내장된 변수 채택 기법을 뜻한다. 모델이 “알아서” feature selection 을 수행하는 것 처럼 비춰질 수 있으나, 사실 정석적인 feature selection 으로 얻는 이점을 곱씹어본다면 (예. 학습 시간 단축 등) 모델링 결과에 기반한 별도 feature selection 과정이 동반되어야 한다는 점은 유사하다고 볼 수 있을 것 같다.

결국 방식에 차이가 있을뿐, 어떠한 feature 가 가장 모델 성능에 기여하는지를 판별하고, 이를 기반으로 데이터를 전처리 하는 과정은 필수적이다! 라고 볼 수 있다.

Regularization

흔히 알려진 Ridge (L2), Lasso (L1), Elastic Net (L1 & L2) 과 같은 회귀식 기반의 regularization 기법이다. 모델 파라미터의 합산값을 손실 함수에 더해, 최소한의 feature 만을 사용한다는 개념이며, 각각 방법론에 따른 행동양식의 차이가 존재한다 - 참고 글.

Random Forest Importance

랜덤 포레스트 모델링 시, feature 별 성능 기여도를 판단할 수 있는 importance 지수 산정이 가능하다. 이 중 가장 대표적인 것이 MDI (Mean Decrease in Impurity) Importance 지수인데, 해당되는 feature 를 기반으로 데이터가 나뉘어질때 감소하는 impurity 의 평균치라고 이해할 수 있다 - 참고 글.