Precision, Recall, F1 스코어 등의 모델 평가 방법

배경

모델 평가 방법에 대한 사전지식이 없는 누군가에게 스팸 필터 모델에 대한 평가를 요구한다면 아마 정확도 (accuracy) 를 평가 기준으로 선택할 것이다. 정확도는 직관적으로 다음과 같이 정의할 수 있다.

$$ \text{Accuracy} = \frac{\text{Number of correct labels}}{\text{Number of all cases}} $$

경우에 따라 정확도는 적절한 평가 지표가 될 수 있겠지만, 문제가 될 여지 또한 존재한다. 예를 들어 데이터셋에 90가지의 비스팸 메일과, 10가지의 스팸메일이 존재한다고 가정한다면, 별도의 수학적 계산 없이 무조건 메일을 비스팸으로 정의하는 더미 모델은 앞서 정의한 정확도가 90% 에 이르게 된다. 따라서 이 경우에 정확도는 모델의 성능 평가라는 목적에 부합하지 않는 지표이다.

다음 글에서는 이러한 Class Imbalance 문제를 해결하기 위해 고안된 기타 평가 지표들을 설명하고있다.

Confusion Matrix

평가 지표 개념을 설명하기 전에 오차 행렬 (Confusion Matrix) 의 개념을 짚고가자. 기본적으로 오차 행렬은 문제 내 존재하는 클래스들의 예측 조합을 보여준다. 예를 들자면 90건의 클래스 Non-Spam 이 Non-Spam 으로 예측된 경우가 82건, Spam 으로 예측된 경우가 8건과 같은 식이다. 아래 그림을 확인하자.


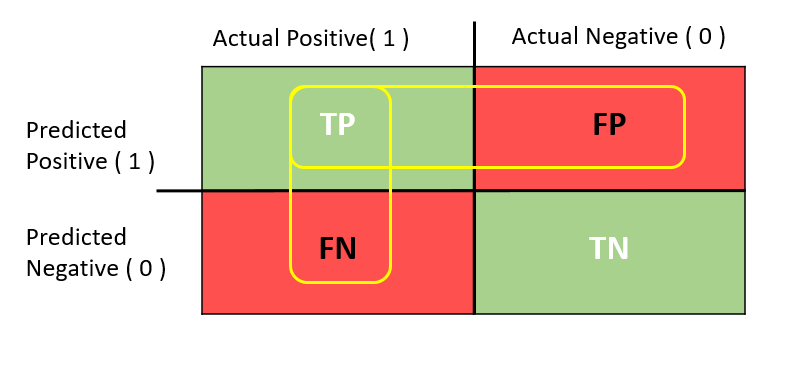
Fig 1. 단순 OX 문제에 대한 오차 행렬

위 그림에서 Positive(1)이 스팸메일을 뜻할 경우 다음과 같은 네가지 경우의 수가 존재한다.

True Positive (TP): 실제 스팸 메일이 스팸 메일로 올바르게 예측된 경우
False Positive (FP): 실제 비스팸 메일이 스팸 메일로 잘못 예측된 경우
False Negative (FN): 실제 스팸 메일이 비스팸 메일로 잘못 예측된 경우
True Negative (TN): 실제 비스팸 메일이 비스팸 메일로 올바르게 예측된 경우

이와 같은 오차 행렬의 언어를 사용하면 Accuracy 지표를 다음과 같이 정의할 수 있게된다.

$$ \text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}} $$

경우의 수가 세분화 되었으니, 유사한 방법으로 성능 평가 지표에 대한 다양한 접근이 가능해졌다. 다음 부분에서는 대표적 대안 지표인 Precision 과 Recall 의 정의를 살펴보자.

Precision & Recall

Precision

Precision 이란 다음과 같이 정의할 수 있다.

$$ \text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} $$

즉, 기존 예시에서 스팸메일로 예측되었던 메일 중 실제 스팸메일의 비율을 나타내는 지표이다. Precision 은 예측이 이미 이루어진 상황에서 예측값의 불순도를 측정하며, 무조건적으로 메일을 비스팸으로 분류하는 더미 모델의 경우 10% 의 Precision Score를 가지게 된다. (여기서 positive(1) 값을 스팸으로 정의하는 것이 중요하다. 스팸 메일과 같은 minority class로 positive(1) 값을 설정해야 class imbalance 문제를 해결할 수 있다).

Precision 이 중요한 지표로 작용하는 예시로는 신선한 야채를 골라내는 분류기가 있다. 골라낸 야채 중 상하고 오래된 야채의 비중이 높을수록 판매자는 여러 심각한 리스크를 떠안게 된다. 신선한 야채를 몇개 버릴지언정 상한 야채를 신선한 야채로 분류하는 비율은 최소한으로 유지해야한다.

Recall

Recall 이란 다음과 같이 정의할 수 있다.

$$ \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} $$

Recall 은 실제 스팸메일 중 스팸메일로 예측된 메일의 비율을 나타내는 지표이다. Recall 스코어는 예측이 이루어지기 전 실제 수치와 예측값의 유사도를 측정하며, 더미 모델의 경우 0% 의 Recall Score를 가지게 된다.

Recall 이 중요한 지표로 작용하는 예시로는 의료적 진단이 있다. 실제 암환자에게 정확한 진단을 내리지 못하는 경우가 많아질수록 환자가 치료시기를 놓칠 위험이 증가하게 된다. 아프지 않은 환자에게 암 진단을 내리는 경우가 생길지언정 실제 암 환자에게 암 진단을 내리지 못하는 비율은 최소한으로 유지해야한다.


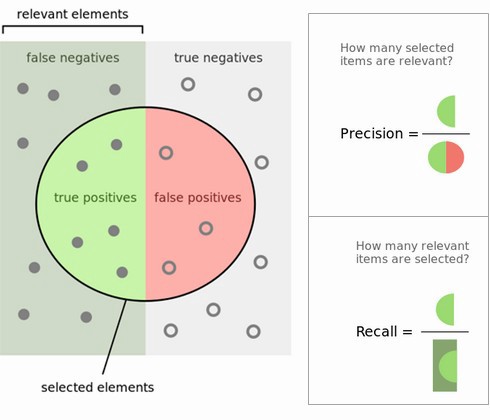
Fig 2. Precision Recall 개념의 이해를 돕는 그림

F1 Score

Precision 과 Recall 을 F1 Score 라는 하나의 지표로 통일하는 방법 또한 존재한다.

$$ \text{F1 Score} = 2 \cdot \frac{\text{Recall} \cdot \text{Precision}}{\text{Recall} + \text{Precision}} $$

Precision 과 Recall 간 조화평균 (Harmonic Mean) 값을 구하는 것인데, 산술평균이나 기하평균이 아닌 조화평균을 사용하는 이유는 Precision 과 Recall 간 분모값 차이로 인한 스케일 차이가 발생하기 때문이다. 참고 설명.

TPR, FPR

TPR (True Positive Rate) 의 정의는 다음과 같으며, Recall 의 정의와 동일하다. 따라서 실제 스팸메일 중 스팸메일로 올바르게 예측된 메일의 비율 을 측정한다.

$$ TPR = \frac{TP}{TP + FN} $$

같은 지표가 TPR 이라는 또 다른 이름은 가지는 이유는 FPR (False Positive Rate) 의 개념과 대비하기 위해서다. FPR 은 다음과 같이 정의되며, 실제 비스팸메일 중 스팸메일로 잘못 예측된 메일의 비율 을 측정한다.

$$ FPR = \frac{FP}{FP + TN} $$

Sensitivity, Specificity

의료 분야에서 주로 사용되는 지표인 Sensitivity 또한 TPR, Recall 의 정의와 동일하며, 실제 스팸메일 중 스팸메일로 올바르게 예측된 메일의 비율 을 측정한다.

$$ \text{Sensitivity} = \frac{TP}{TP + FN} $$

Sensitivity 는 Specificity 의 다음 정의와 대비되며, 실제 비스팸메일 중 비스팸메일로 올바르게 예측된 메일의 비율 을 측정한다. 즉, FPR 이 비스팸메일 데이터의 오류에 대한 비율이라면 Sensitivity 는 정확도에 대한 비율이라고 이해하면 된다. 같은 분모를 가지고 있지만 다른 분자를 가지고 있는 것을 확인할 수 있다.

$$ \text{Specificity} = \frac{TN}{FP + TN} $$

PR Curve, ROC Curve


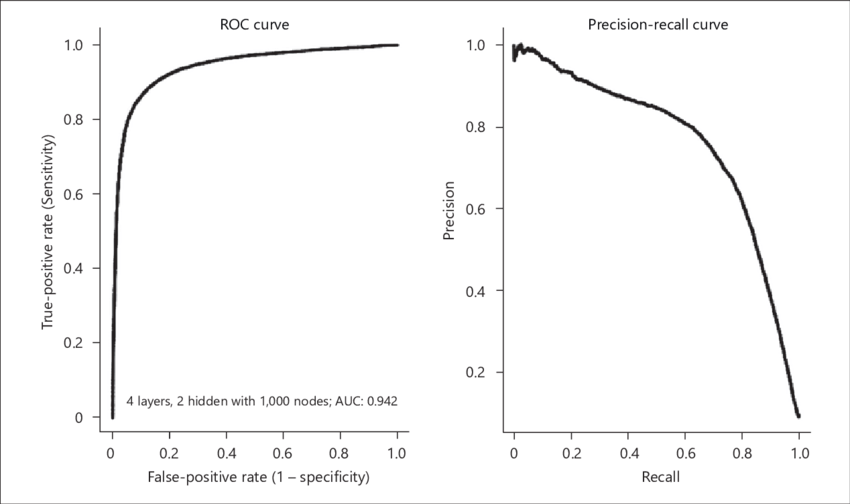
Fig 3. 분류기 모델의 ROC, PR Curve 예시

Precision-Recall (PR) Curve

“신선한 야채를 몇개 버릴지언정”, “아프지 않은 환자에게 암 진단을 내리는 경우가 생길지언정” 과 같은 말은 이 두개 지표 사이에 trade-off 관계가 있음을 암시한다.

더미 모델이 아닌 실제 각 클래스에 속할 확률을 구하는 모델의 경우, 확률이 몇퍼센트 이상일때 positive(1) 으로 분류할 것인가를 정의하는 threshold 파라미터를 가지고 있게된다 (30% 이상의 확률일때 스팸으로 분류, 50% 이상의 확률일때 스팸으로 분류 등). 이 threshold 를 움직임에 따라 Precision Recall 지표값이 어떠한 상관관계를 가지고 있는지를 나타내는 그래프를 Precision-Recall Curve, 혹은 PR Curve 라 칭한다.

위의 예시와 같이 일반적인 분류기는 Precision 이 상승하면 Recall 이 하락하고, Recall 이 상승하면 Precision 이 하락하는 관계를 가지고 있다.

ROC Curve

Receiver Operating Characteristic (ROC) Curve 또한 동일하게 threshold 의 움직임에 따라 TPR, FPR 지표의 상관관계를 나타내는 그래프이다. PR Curve 와는 반대로 하나의 지표가 상승할때 다른 하나의 지표 또한 같이 상승하는 관계를 가지고 있으며, 이는 TPR 은 정확도에 대한 지표인 반면 FPR 은 오류율에 대한 지표이기 때문이라고 이해하면 된다.

이상적인 모델은 ROC Curve 의 좌상단에 위치한, 즉 1의 TPR과 0의 FPR을 가지고 있는 모델이다. 이는 스팸메일은 항상 스팸메일로, 비스팸메일은 항상 비스팸메일로 분류하는 모델을 뜻하기 때문이다.

Area Under the Curve

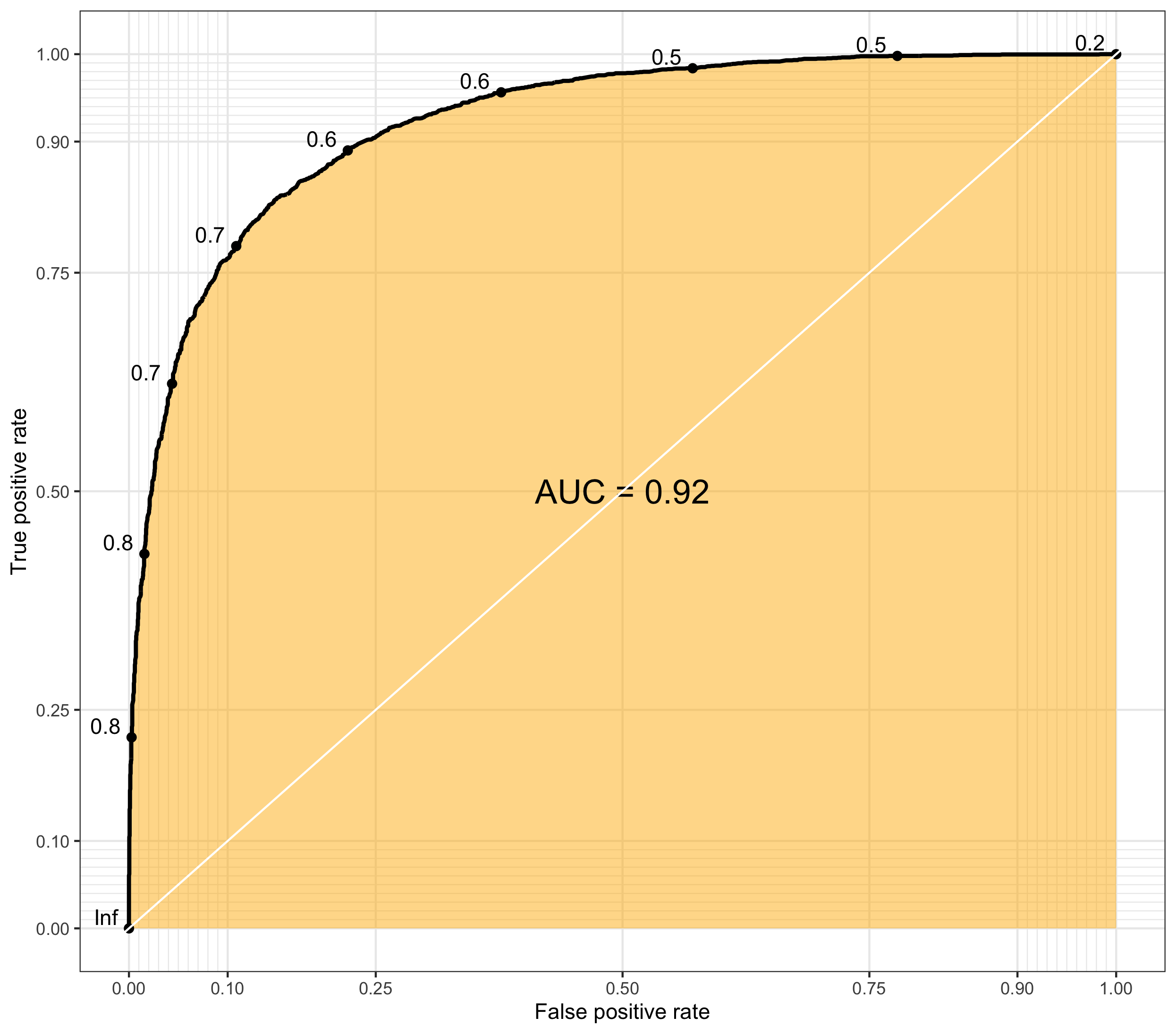
Area Under the Curve (AUC) 는 말 그대로 적분을 통해 PR Curve 와 ROC Curve 의 부피를 구한 값이다. 어떤 그래프의 부피인가에 따라 ROC-AUC, PR-AUC 로 정의되며, 모델 평가에 가장 일반적으로 쓰이는 지표는 ROC-AUC 이다. AUC 는 (0, 1) 의 범위를 가지고 있기 떄문에 ROC-AUC, PR-AUC 모두 1에 가까울수록 정확도가 높은 분류기로 정의할 수 있다.


Fig 4. 분류기 모델의 ROC-AUC 예시