Singular Value Decomposition 의 개념 소개

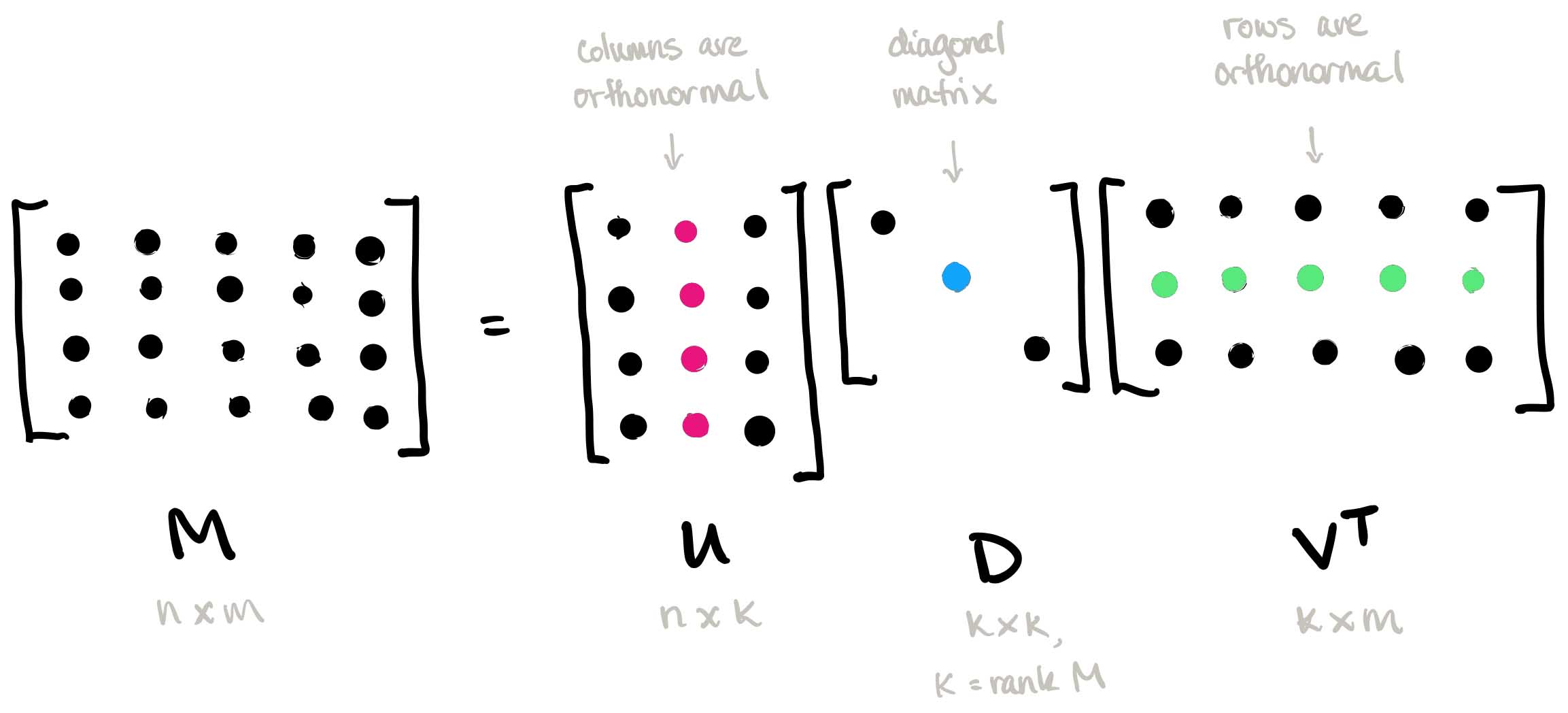
Introduction

공돌이의 수학정리노트 블로그를 인용하자면, 특이값 분해가 설명하고자 하는 바는 “직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게 되는 그 직교 집합은 무엇인가? 그리고 선형 변환 후의 결과는 무엇인가?” 로 정리할 수 있다.
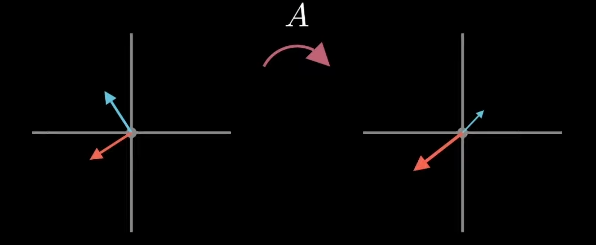
시각적인 설명은 덧붙이자면, 왼편의 직교하는 벡터 집합 $V$ 에 대한 $A$ 매트릭스 선형 변환 결과를 오른편의 벡터 집합 $U\Sigma$ 라고 가정.


Fig 1. 직교성 조건을 만족하지 못하는 경우

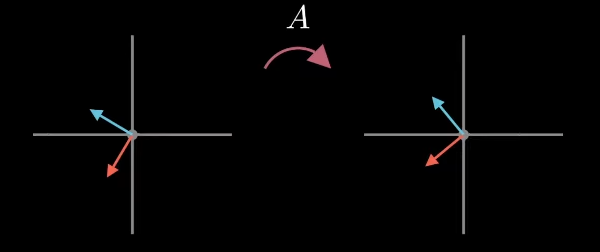
시각화를 돕기 위해 오른편의 벡터 크기를 의미하는 $\Sigma$ 매트릭스를 제외한 후, 다음과 같은 결과를 만족하는 크기 1 의 벡터 집합 $U$ 을 찾는 과정이다.


Fig 2. 직교성 조건을 만족하는 경우

즉, 각자 직교하는 벡터 집합 $U, V$ 는 다음과 같은 관계를 가진다.

$$ AV = U\Sigma $$

특이값 분해의 정의

임의의 $m \times n$ 차원 행렬 $A$ 를 다음과 같이 분해하는 행렬 분해 방법 중 하나이다.

$$ A = U\Sigma V^T $$

네 행렬 ($A, U, \Sigma, V$) 의 크기와 성질은 다음과 같이 정리할 수 있다.

$$ A: m \times n \text{ regular matrix} \newline U: m \times m \text{ orthogonal matrix} \newline \Sigma: m \times n \text{ diagonal matrix} \newline V: n \times n \text{ orthogonal matrix} $$

Orthogonality 란 컬럼 별 벡터가 모두 서로 직교하는 성질을 칭하는데, 소개 섹션에서 언급했듯 이는 매트릭스 $A$ 에 의해 변환되는 두 개 벡터 집합 $U$ 와 $V$ 의 기본 전제이다.
이러한 Orthogonal 매트릭스는 또한 다음과 같은 성질을 가진다.

$$ UU^T = U^T U = I $$

$$ U^{-1} = U^T $$

따라서 다음과 같은 유도가 가능한 것.

$$ AV = U\Sigma \newline = AVV^T = U\Sigma V^T \newline = A = U\Sigma V^T $$

Diagonality 란 행렬의 대각성분을 제외한 나머지 원소의 값이 모두 $0$ 인 경우를 뜻한다.
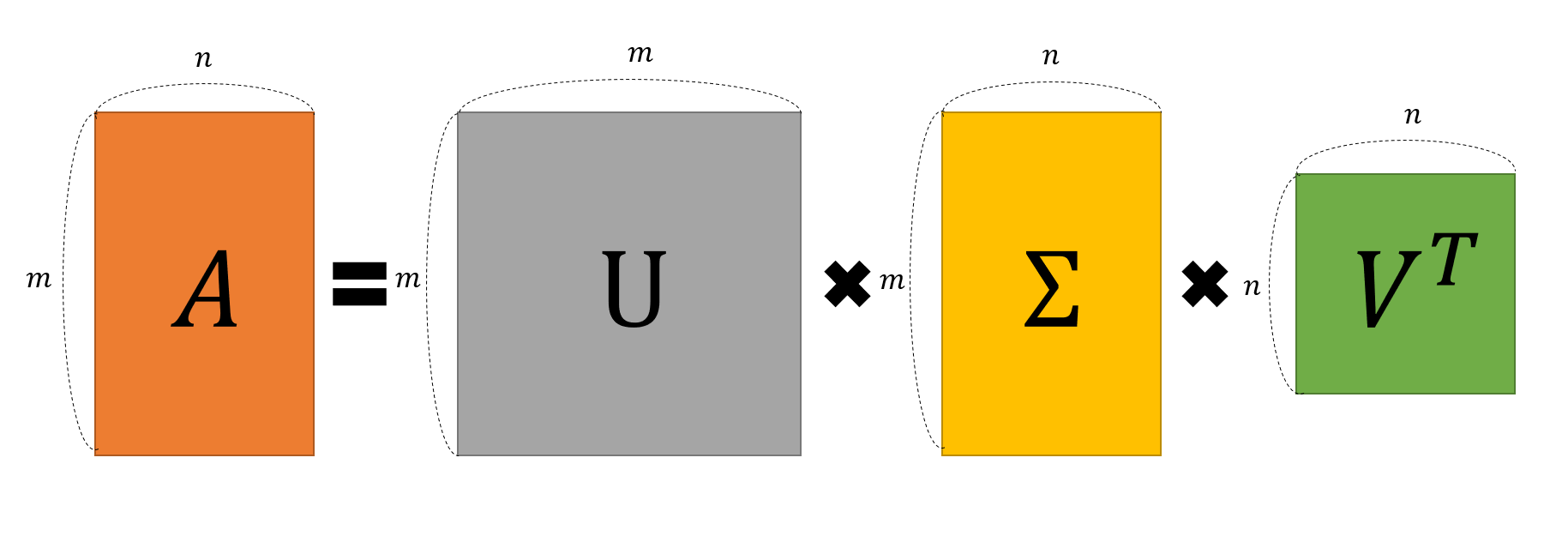
Diagonal Matrix 를 $m \times n$ 모양으로 가정했을 때 행렬 크기가 맞지 않는 애매한 경우가 발생할 수 있다. 이럴때 $m > n$ 인 경우 $n \times n$ 행렬 하단에 모든 원소가 $0$ 인 $m - n \times n$ 행렬이 붙어있게 되거나, $m < n$ 인 경우 $m \times m$ 행렬 오른쪽에 모든 원소가 $0$ 인 $n \times n - m$ 행렬이 붙어있는 식.


Fig 3. 특이값 분해 방정식 내 행렬 도식화

U 와 V 를 어떻게 찾을까?

우선 다음과 같이 행렬 $A$ 와 $A^T$ 를 정의하자.

$$ A = U\Sigma V^T \newline $$

$$ A^T = (U\Sigma V^T)^T = V\Sigma^T U^T $$

이를 활용해 다음과 같은 수식 관계를 찾을 수 있다.

$$ AA^T = U\Sigma V^TV\Sigma^T U^T = U\Sigma^2 U^T $$

$$ A^T A = V \Sigma^T U^T U\Sigma V^T = V \Sigma^2 V^T $$

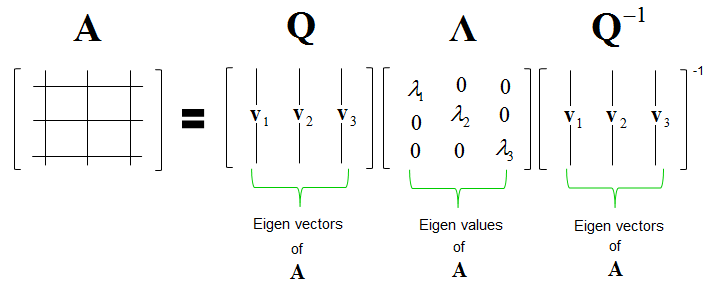
즉, 벡터 집합 $U$ 와 $V$ 는 각각 $AA^T, A^TA$ 행렬에 대한 eigenvector 이며, 이는 eigendecomposition 테크닉을 활용해 풀이가 가능하다. 관련한 컨텐츠는 3blue1brown 과 ritvikmath 비디오 참고.


Fig 4. 고유값 분해 (Eigen-decomposition) 방정식

특이값 분해의 목적과 활용

특이값 분해의 공식은 다음과 같이 풀어쓰는 것이 가능하다.

$$ A = U\Sigma V^T $$

$$ = { \begin{pmatrix} | & | & & | \newline u_1 & u_2 & \cdots & u_m \newline | & | & & | \end{pmatrix} \begin{pmatrix} \sigma_1 & & & & 0 \newline & \sigma_2 & & & 0 \newline & & \ddots & & 0 \newline & & & \sigma_m & 0 \newline \end{pmatrix} \begin{pmatrix} - & v_1^T & - \newline - & v_2^T & - \newline & \vdots & \newline - & v_n^T & - \newline \end{pmatrix} } $$

$$ = \sigma_1 u_1 v_1^T + \sigma_2 u_2 v_2^T + … + \sigma_m u_m v_m^T $$

$u_1 v_1^T$ 등의 결과값은 $m \times n$ 행렬이며, 합산을 통해 최종 행렬인 $A$ 에 다다르기 위한 하나의 레이어 정도로 생각할 수 있다. $u$ 와 $v$ 는 정규화된 벡터이기 때문에 $u_1 v_1^T$ 의 값은 1 과 -1 사이에 위치한다.
따라서 $u_1 v_1^T$ 에 의해 특정된 레이어의 정보량은 $\sigma_1$ 에 의해 정해지며, 이를 특이값이라 부른다.
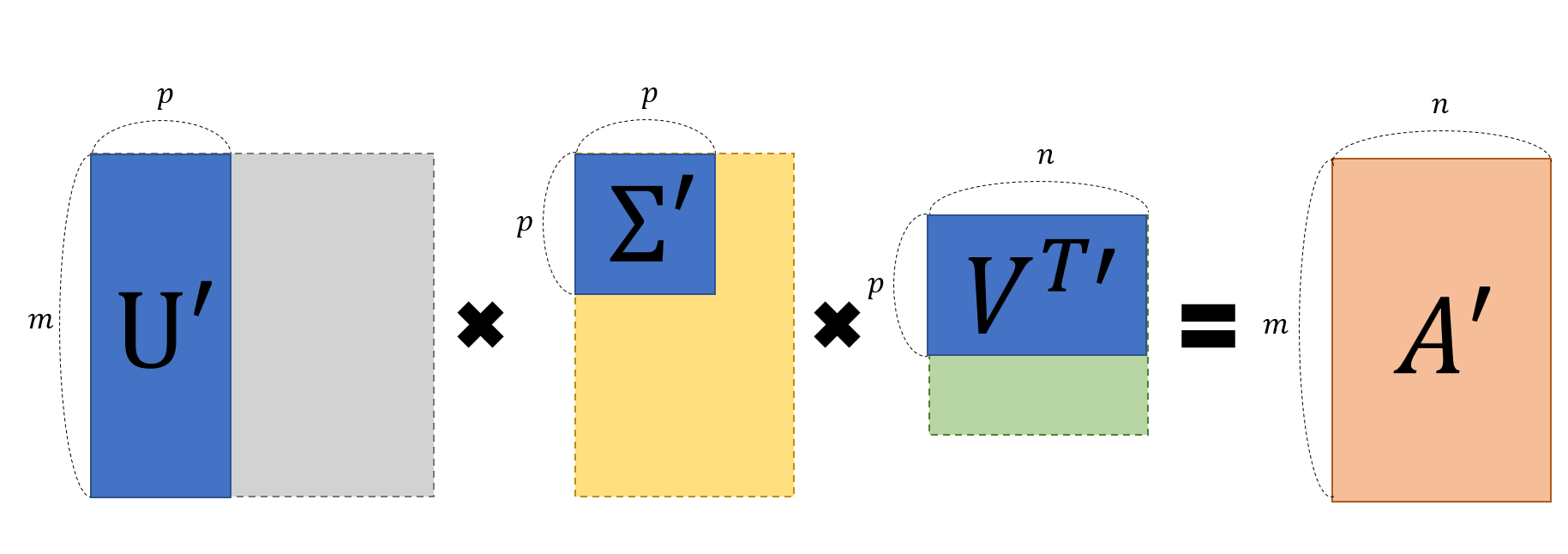
레이어 별 정보량은 특이값의 크기에 의해 결정되기 때문에, 특이값 $p$ 개 만을 이용해 행렬 $A$ 를 부분 복원하는 작업이 가능해진다.


Fig 5. 행렬 $A$ 의 부분 복원 과정 도식화

이를 가장 직관적으로 설명하는 방법은 이미지의 SVD 복원 과정을 시각화하는 것이다. 하단의 예시는 이미지를 다수의 레이어로 분할 후, 레이어의 누적 합을 단계적으로 시각화 한 것이다. 초반 몇개의 레이어에 주요 정보들이 집중되어 있고, 후반 레이어로 갈수록 마이너한 정보를 담고 있다. 이는 $\Sigma$ 행렬에서 특이값 $\sigma_x$ 이 계속해 작아지며, 이에 상응하는 $u_x v_x^T$ 레이어가 가진 정보량이 감소하는 것과 같은 원리.


Fig 6. 공돌이의 수학정리노트 블로그에 소개된 SVD 복원 예시

차원축소 기법과의 연계점

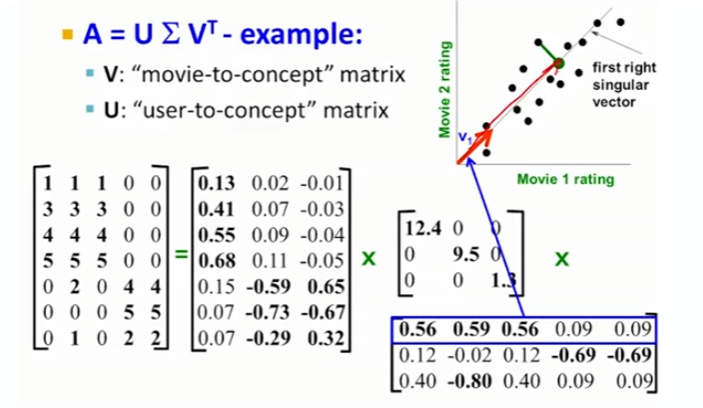
$A$ 행렬에서 분해된 $U, \Sigma, V$ 행렬 중, $V$ 행렬의 각 row vector 는 projection axis, 즉 차원 축소를 수행할 축을 특정하며, 이에 상응하는 $\Sigma$ 행렬의 원소는 해당 projection axis 의 정보량을 특정한다. 하단 예시에서 파란색으로 표기된 $v_1$ axis 의 정보량은 $\sigma_1 = 12.4$ 와 같은 식.


Fig 7. $v_1$ 벡터는 $\sigma_1$ 만큼의 정보량을 가지는 projection axis 를 특정한다

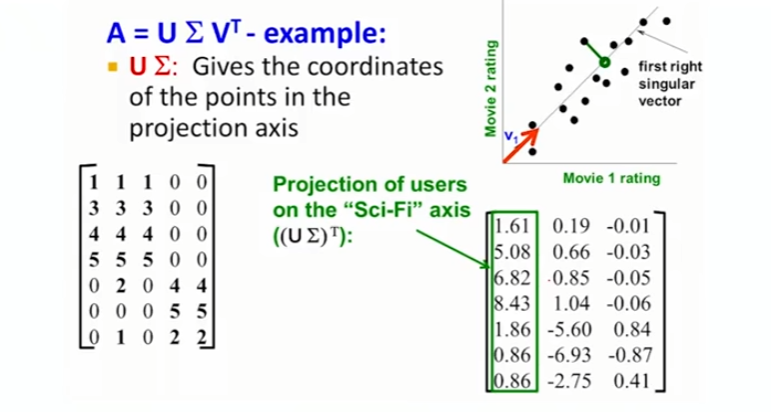
Projection axis 가 특정 되었다면, 해당 projection axis 에 데이터를 투영했을때 각 데이터가 가지는 값은 행렬곱 $U\Sigma$ 에 의해 결정되게 된다.


Fig 8. 차원 축소 후 데이터의 위치는 $U\Sigma$ 에 의해 결정

본격적인 차원 축소를 수행하기 위해서는 먼저 축소 차원 수 $n$ 을 결정한 후, $\Sigma$ 행렬에서 가장 큰 특이값 $n$ 개를 제외한 나머지 값을 $0$ 으로 바꿔주어야 한다.


Fig 9. 차원 축소 수행을 위해서는 가장 작은 특이값 n 개를 0 으로 설정