배치정규화 (Batch Normalization) 란?

TL;DR

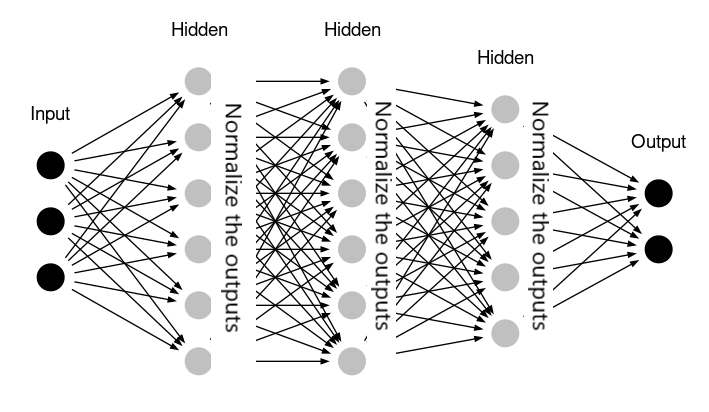
딥러닝 모델의 mini-batch 학습은, 학습 단계 별 데이터의 분포가 서로 다르다는 점에서 그 복잡성이 올라가고는 한다. 배치정규화 논문이 공개되기 전에는 이 문제를 해결하기 위해 단순히 input data $X$ 를 정규화 하는것에 그쳤으나, 해당 논문을 개재한 Google 팀은 각 중간 레이어의 아웃풋에 또한 정규화를 적용함으로 모델의 학습속도를 끌어올릴 수 있다는 점을 발견했다. 이와 같은 레이어 별 정규화 과정은 배치 스텝마다 별도로 적용되어야 하며 (input data $X$에 대한 정규화는 전체 분포에 대한 정보가 있기때문에 일괄적으로 이루어질 수 있지만 중간 레이어의 결과값은 그렇지 못함), 따라서 이를 배치정규화라 칭한다.

Internal Covariate Shift

Google 팀이 중간레이어의 아웃풋을 정규화하게 된 배경에는 그들이 internal covariate shift 라고 명명한 문제가 존재한다. 비신경망 머신러닝 모델에 서로 다른 분포를 가진 데이터를 넣을떄 발생하는 covariate shift 라는 문제를 중간레이어 개념에 도입한 것인데, 특히 hyperbolic tangent, sigmoid와 같은 비선형 활성화 함수 (non-linear activation function) 를 무겁게 사용하는 딥러닝 모델의 경우 이와 같은 분포 차이에 취약해질 여지가 많다.

$$ g(x) = \frac{1}{1 + e^{-x}} $$

위의 sigmoid 함수에서 input 값 $x$가 조금만 올라가거나 내려가도 학습 속도는 기하급수적으로 느려지게된다는 점을 기억할 것이다 (함수의 결과값이 0에 가까워지며 그 기울기가 작아지기 때문). 분포차가 심한 데이터를 단계별로 학습할때 이와 같은 문제로 인해 convergence를 찾는 과정이 심각하게 느려질 수 있다.

또 하나의 문제는 레이어를 통과할수록 배치 간 데이터의 분포가 점차 더 큰 차이를 가지게 된다는 점이다. 신경망 구조가 워낙 복잡하기도 하지만, 이전 레이어의 가중치 (weight) 와 편향 (bias) 이 학습과정에서 계속 업데이트 되기 때문인데, 이쯤되면 중간레이어의 정규화 없이 학습이 이루어진다는게 오히려 이상하게 보인다.

방법론

일반적인 배치정규화는 activation function 의 아웃풋 $a$ 가 아닌 인풋 $z$ 에 적용된다. 비교적 일정하고, 적정한 범위내의 데이터를 activation function 에 집어넣어 activation layer 내 가능한 많은 노드가 제 역할을 하게하자는 취지이다. 한 개 레이어에서 배치정규화를 수행하는 방법은 다음과 같다.

$$ \mu = \frac{1}{m} \sum_{i} z^i $$

$$ \sigma^2 = \frac{1}{m} \sum_{i} (z_i - \mu)^2 $$

우선 선형함수 $z$ 의 평균 $\mu$ 와 분산 $\sigma^2$ 를 구한다. 해당 값들은 레이어, 배치 별로 그 값이 다르기 때문에 학습, 예측 단계에서 매번 계산이 필요하다.

$$ z_{norm}^i = \frac{z^i - \mu}{\sqrt{\sigma^2 + \epsilon}} $$

정규화 수식을 이용하여 $z_{norm}$ 값을 구한다. 여기서 수식의 분모에 있는 $\epsilon$ 은 $\sigma^2$ 가 $0$ 일 경우에 대비한 아주 작은 safety term 이다. 이로 인해 $z_{norm}$ 은 평균이 $0$ 이며, 표준편차가 $1$ 에 해당하는 분포를 가지게된다.

Input에 대한 정규화 처리는 이 단계에서 끝나겠지만 배치정규화는 다음과 같이 평균값과 표준편차에 대한 자유도를 주게된다. 처음 접했을때 다소 헷갈렸던 부분인데 데이터에 관계 없이 고른 분포를 추출하는 과정이라고 생각하면된다.

$$ \tilde{z^i} = \Gamma z_{norm}^i + \Beta $$

여기서 $\Gamma$ 와 $\Beta$ 는 학습을 통해 최적값에 수렴하게된다. 이후 레이어, 배치 별 정규화가 적용된 $\tilde{z^i}$ 를 활성함수의 인풋으로 사용하면 배치정규화가 적용된 것이다.

기타 효과

구체적으로 배치정규화가 모델의 학습과정을 개선시키는 방법은 다음과 같이 정리할 수 있다.

1. 학습 속도 개선

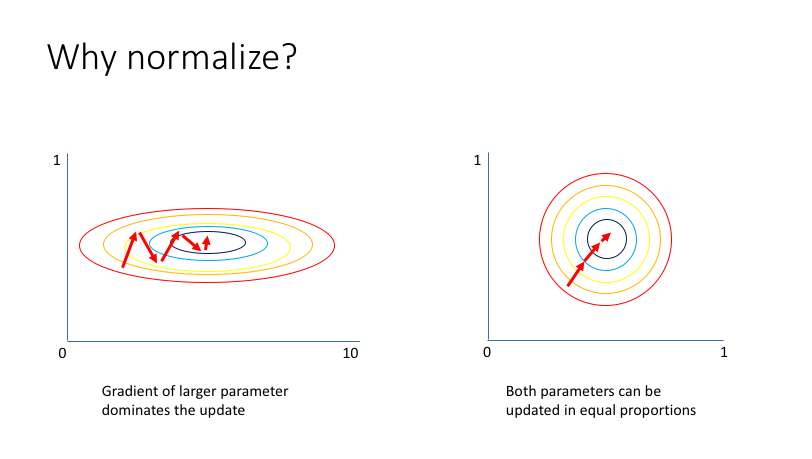
alt text

정규화된 분포는 어떻게 학습 속도를 개선할까? 위 그림에서 왼쪽 그래프는 정규화가 적용되지 않은 경우의 손실함수를, 오른쪽 그래프는 정규화가 적용된 경우의 손실함수를 시각화 하고있다. 왼쪽의 경우 전반적인 손실함수 결과값이 $x$ 축 변수보다 $y$ 축 변수의 움직임에 더 민감한 부분을 확인할 수 있는데, 따라서 큰 학습속도 $\alpha$ 를 적용할 경우 방향성을 잃어 최적값을 찾지 못하는 문제가 발생할 여지를 가지게 된다. 두 변수의 스케일 차이가 학습률에 제약을 가져오는 것이다.

반면 오른쪽 그래프에서는 손실함수의 결과값이 두 개 변수에 유사한 민감도를 가지고 있는 점을 확인할 수 있다. 물론 이 경우 또한 지나치게 큰 $\alpha$ 값은 문제를 야기하겠지만, 전자의 경우에 비해 그 정도가 개선되었다는 점을 독자는 시각적으로 확인이 가능할 것이다.

2. 초기값에 대한 내성

위 그림을 다시 참조하자. 왼쪽 그래프의 경우 초기값이 타원의 오른쪽 끝에 있을 경우와, 중하단에 있을 경우 중심점 (최적값) 으로 부터의 상당한 거리차가 발생한다. 이는 모델의 초기값에 따른 학습속도 차이가 발생할 수 있음을 의미한다. 오른쪽 그래프 또한 이러한 문제점을 어느정도 안고 있지만, 적어도 동일한 붉은 원 안에서는 거리차가 발생하지 않는다는 점을 확인할 수 있다.