수학적으로 이해하는 최적화 기법

TL;DR

경사하강법이란 여러개의 변수를 활용해 정의된 머신러닝 모델의 손실함수 (Loss Function) 를 최저치로 낮추는 기법이다. 변수 $i$ 에 대한 손실함수 $J$ 의 미분값을 $\alpha$, 혹은 학습률 (learning rate) 로 불리는 학습 속도 설정값에 곱한 후, 변수 $i$ 에 적용되는 가중치 $\theta_i$ 에서 빼주는 방식이다. 수식은 다음과 같이 정의된다.

$$ \theta_i := \theta_i - \alpha \frac{\partial}{\partial \theta_i}J(\theta) $$

다만 mini-batch 경사하강의 경우 매 iteration에서 리소스적인 문제로 전체 데이터가 아닌 부분 데이터를 활용하기 때문에 여기서 하강이 이루어지는 방향이 직진성을 띄고 있지 않을 가능성이 높은데, 모멘텀은 이러한 문제를 해결하기 위해 변수 별 미분값의 점진적 평균값 (지수 가중 평균) 을 구해 하강의 방향성을 찾는다.

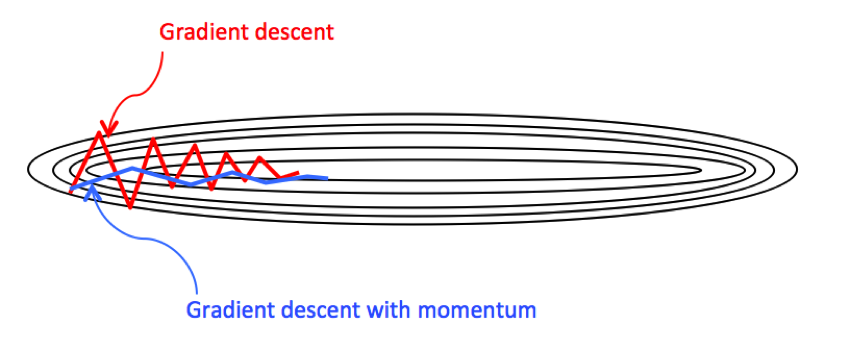
alt text

위 그림에서 y축 변수의 하강 방향은 지그재그 형태를 띄는 반면, x축 변수의 하강 방향은 일정한 방향성을 띄고있다. 이로 인해 기본적인 형태의 경사하강 진행 시 학습 과정이 불필요하게 길어지게되는 결과를 야기하게되나, 모멘텀 최적화 방식을 이용하면 y축 변수 하강 방향의 점진적 평균은 0에 가까워지며, x축 변수 하강 방향의 점진적 평균값은 유지되기 때문에 불필요한 학습 과정이 줄어드는 (직진성) 효과를 가진다.

RMSProp은 유사하지만 평균치가 아닌 제곱평균제곱근 (RMS) 을 통해 그 방향성을 구하고자하며, ADAM 은 이 두가지 최적화 방식의 조합이다.

지수 가중 평균의 정의 (Exponentially Weighted Averages)

개념 및 정의

위 세개의 최적화 개념을 수학적으로 이해하기 위해서는 지수 가중 평균 (EWMA) 개념을 먼저 이해할 필요가 있다. 개념은 생각보다 복잡하지 않은데, $\theta_1,\theta_2, \theta_3, … , \theta_n$ 와 같이 순차적인 $n$개의 데이터셋이 있을 시 $n$ 보다 작거나 같은 시점 $t$ 의 지수 가중 평균 $V_t$는 다음과 같이 정의된다.

$$ V_0 = 0；　 V_t = \beta V_{t-1} + (1-\beta)\theta_t $$

여기서 $\beta$ 값은 사용자가 지정하며 (가장 일반적인 값은 $0.9$ 이다), 이렇게 계산된 $V_t$ 값은 대략 $t - \frac{1}{1 - \beta}$ 부터 $t$ 까지 기간의 단순 평균치에 근접하게 된다. 누적된 평균값에 일정 비율로 현재 값을 반영하는 접근법이며, Bayesian 통계와 개념적으로 유사한 부분이 있다.

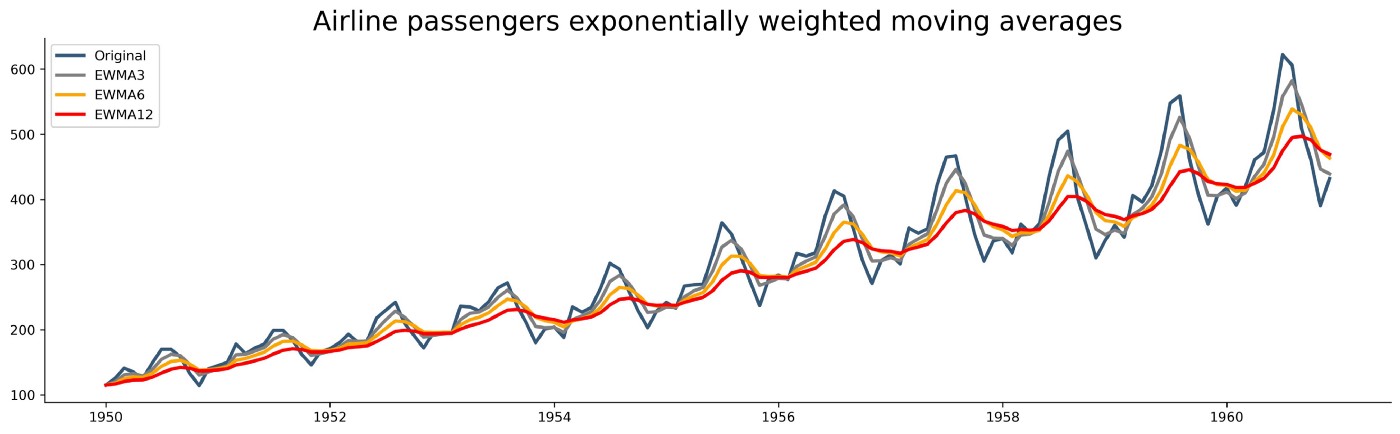
아래 그래프는 파란색으로 표기된 Original 데이터에 조금씩 큰 $\beta$ 값을 사용하며 계산한 EWMA 를 시각화한 결과이다. 회색이 가장 낮은 $\beta$, 빨간색이 가장 높은 $\beta$ 에 해당하는데, $\beta$ 값이 높을수록 과거 데이터에 큰 영향을 받으며 신규 데이터에 대한 적응 딜레이가 생기는 점이 확인 가능하다.

alt text

Bias Correction

예리한 독자라면 알아챘겠지만, 위 알고리즘을 그대로 적용할 시 초반 $V_t$ 값은 거의 $0$ 에 근접한 값이 나오게 된다.

더 나은 방법은 $V_t$ 를 $\frac{V_t}{1 - \beta^t}$ 로 스케일링하는 것이다. 이로 인해 실제 데이터와 다르게 $0$ 에 가까웠던 작은 $t$ 영역의 값은 큰 폭으로 상향되고, 큰 $t$ 영역의 값은 별다른 영향을 받지 않게 된다. 이와 같이 적절한 초기 값을 부여함으로 인해 값이 작은 $t$ 영역의 EWMA 값을 실제 데이터와 유사하게 바꿀 수 있으며, 이를 Bias Correction 이라고 한다.

Momentum

TL;DR 섹션에서 첨부한 이미지를 다시 보자. 붉은색 경사하강은 지그재그 방향으로 움직이고 있기 떄문에 파란색 경사하강을 유도하기 위해서는 y축 움직임을 최소화하고, x축 움직임을 최대화해야 한다. 여기서 우리는 EWMA 개념을 다음 pseudo code와 같이 적용한다 ($w_i$ 는 $i$ 변수에 적용되는 가중치를 의미).

1
2
3
4
5
6


 on interation t:
    compute dy, dx on current mini-batch
    V_dy = beta * V_dy + (1 - beta) * dy
    V_dx = beta * V_dx + (1 - beta) * dx
    w_y = w_y - alpha * V_dy
    w_x = w_x - alpha * V_dx

해당 로직을 적용하면 y축 변수는 음수와 양수 사이를 반복적으로 움직이기 때문에 점차 $0$ 에 가까운 EWMA 값에 수렴하게 되며, x축 변수는 계속해 양수 방향으로 움직이기 때문에 EWMA 값은 양수 방향을 유지하게 된다.

한 가지 유념해야 할 부분은, 경사하강법에 모멘텀을 적용하게 되면 기존에는 없던 $\beta, \alpha$ 두 개 하이퍼파라미터가 발생하게 된다는 점이다. 앞서 언급했듯 초기 $\beta$ 값은 $0.9$ 정도로 세팅하는 것이 세월에 따른 검증을 통해 권장되고 있으며, 이는 대략 과거 10개 iteration 의 평균 미분값에 해당하게 된다. Bias correction 의 경우 초기 iteration 에서만 영향을 끼치기 때문에 실제 모델링 시 생략되는 경우가 많다.

RMSProp

RMSProp (Root Mean Squared Prop) 은 모멘텀과 유사하게 경사하강의 방향성을 찾는 알고리즘이다. 구체적인 설명에 들어가기 전 다음 pseudo code를 확인하자.

1
2
3
4
5
6


 on interation t:
    compute dy, dx on current mini-batch
    S_dy = beta * S_dy + (1 - beta) * (dy ** 2)  # element-wise square
    S_dx = beta * S_dx + (1 - beta) * (dx ** 2)  # element-wise square
    w_y = w_y - alpha * ( dy / (sqrt(S_dy) + epsilon) )
    w_x = w_x - alpha * ( dx / (sqrt(S_dx) + epsilon) )

모멘텀 알고리즘이 $V_{dy}$ 와 $V_{dx}$ 값을 업데이트하기 위해 변수 별 미분값 $d_y$ 와 $d_x$ 을 그대로 사용했던 것과 달리, RMSProp 알고리즘은 두 미분값의 제곱을 사용하고 있다. 자연스럽게 y축 변수는 위아래로 큰 움직임을 가지고있기 때문에 $d_y$ 의 제곱값의 누적치는 큰 결과값을 가지게 되며 (x축 변수의 경우 반대로 작은 결과값), 이러한 누적치의 제곱근을 $d_y$ 에서 나누어줌으로써 경사하강 과정에서 $w_y$ 를 상대적으로 작은 값으로 업데이트하게 된다 (x축 변수의 경우 상대적으로 큰 값).

$\epsilon$ 은 단순한 safety term 정도로 이해하면 되는데, $\sqrt{S_{dy}}$ 값이 0이 될때 $\frac{d_y}{\sqrt{S_{dy}}}$ 이 무한대로 커지는 경우를 방지하기 위해 $\epsilon = 10^{-8}$ 라는 식의 아주 작은 값을 대입하는 것이라고 이해하면 된다. 개념적인 설명이 길어 어렵게 느낄 수 있지만, 천천히 위 코드의 진행과정을 읽어보며 설명을 참조하면 단순히 모멘텀 알고리즘에 단순평균이 아닌 RMS 개념을 도입했다는 것을 이해할 수 있을 것이다.

여담으로 한가지 재밌는 점은 RMSProp 알고리즘의 경우 학술적인 논문이 아닌 Turing Award 수상자 Geoffrey Hinton 교수가 토론토 대학에서 가르치던 수업에서 제안한 모멘텀 알고리즘의 대안으로 처음 알려지게 되었다는 점이다. 관심이 있다면 본 링크에서 해당 수업의 파워포인트 슬라이드를 확인할 수 있다.

ADAM

모멘텀 알고리즘, RMSProp 알고리즘까지 개념적인 이해가 이루어졌다면 바로 다음 ADAM (Adaptive Moment Estimation) Optimizer 알고리즘을 이해할 수 있을 것이다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


 on interation t:
    compute dy, dx on current mini-batch
    V_dy = beta_1 * V_dy + (1 - beta_1) * dy
    V_dx = beta_1 * V_dx + (1 - beta_1) * dx
    S_dy = beta_2 * S_dy + (1 - beta_2) * (dy ** 2)  # element-wise square
    S_dx = beta_2 * S_dx + (1 - beta_2) * (dx ** 2)  # element-wise square

    V_dy = V_dy / (1 - beta_1 ** t)
    V_dx = V_dx / (1 - beta_1 ** t)
    S_dy = V_dy / (1 - beta_2 ** t)
    S_dx = V_dx / (1 - beta_2 ** t)

    w_y = w_y - alpha * ( V_dy / (sqrt(S_dy) + epsilon) )
    w_x = w_x - alpha * ( V_dx / (sqrt(S_dx) + epsilon) )

모멘텀의 $V$ 값, RMSProp의 $S$ 값을 개별적으로 구한 후, 각각 bias correction 이 이루어진 $V$ 값에서 $S$ 값의 제곱근을 나눈 결과를 기반으로 경사하강을 진행하는 방식이다. 반복적인 실험을 통해 일반화가 가능할 정도로 그 효과성이 검증되었으며, $\beta_1$ 의 경우 $0.9$, $\beta_2$ 의 경우 $0.999$, $\epsilon$ 의 경우 $10^{-8}$ 의 초기값을 기본으로 하고있다. $\alpha$ 값의 경우 모델에 따라 기본적인 튜닝을 필요로 한다.

PyTorch, Keras, Tensorflow 와 같은 메이저한 딥러닝 프레임워크는 당연히 ADAM Optimizer, RMSProp, 모멘텀과 같은 최적화 알고리즘을 기본으로 제공하고 있으며, 이러한 최적화 알고리즘의 작동방식과 각 하이퍼파라미터의 의미를 정확하게 알고있다면 보다 효율적인 모델링이 가능할 것이다.