PyTorch Deep Learning

소개

신경망을 수학적으로 구현함에 있어 가장 까다로운 부분은 역전파 (backpropagation) 과정이다. 짧게 설명하자면, 모델에 존재하는 각각의 가중치(weight)와 편향(bias)이 손실함수에 어떠한 영향을 끼치는지를 연산한 다음, 이 정보를 활용해 가중치와 편향의 값을 손실함수를 줄이는 방향으로 갱신시키는 과정이다. 개념적인 이해가 필요하다면 앞선 역전파 해시넷 링크와 더불어 1번, 2번 비디오를 참고하자.

역전파 과정에서 가장 중요한 수학적 요소는 손실함수에 대한 가중치와 편향의 편미분 (partial derivative) 연산이다. 가중치가 증가할때 손실함수 또한 같이 증가한다면 가중치값을 내리고, 편향 값이 내려갈때 손실함수가 증가한다면 반대로 편향값을 증가시키는 식이다. 이러한 과정을 반복함으로 인해 모델은 가능한 낮은 손실함수, 즉 높은 정확도를 가지게 된다.

하지만 신경망 네트워크에는 경우에 따라 수십만개의 가중치와 편향이 존재하고, 이를 학습 사이클마다 일일이 손으로 계산할 수 없기 때문에 편미분 연산을 자동적으로 처리해주는 알고리즘을 필요로 하게 되었다. 주요 딥러닝 프레임워크인 PyTorch 의 Autograd 패키지는 이러한 역전파 과정을 자동적으로 처리해주는 기능을 가지고있다.

자동 미분 (Automatic Differentiation)

Autograd 패키지를 소개하기에 앞서, 자동 미분이 어떠한 방식으로 이루어지는지를 우선 살펴보고자 한다. 자동 미분의 접근 방식은 크게 세가지 (Numerical, Symbolic, Automatic) 가 존재한다.

a. Numerical

Numerical 접근은 고등학교 수학에서 등장하는, 극한을 통한 미분의 정의를 이용한다. $f(x)$가 input vector $x$에 대한 손실함수라고 가정했을때의 공식은 다음과 같다.

$$ \begin{align} \frac{\delta f}{\delta x_i} = \lim_{h \to 0} \frac{f(x+he^i) - f(x)}{h} \end{align} $$

여기서 $x$란 길이 $n$의 input 벡터이며, $e^i$ 란 길이가 $n$이며 $i$ 번째 값이 1, 나머지 값이 0인 단위벡터 (unit vector) 이다.

$$ \begin{align} x = \begin{bmatrix} x_1 \ x_2 \ \dots \ x_n \end{bmatrix} ; \ e^1 = \begin{bmatrix} 1 \ 0 \ \dots \ 0 \end{bmatrix} ; \ e^2 = \begin{bmatrix} 0 \ 1 \ \dots \ 0 \end{bmatrix} ; \ \dots \end{align} $$

따라서 (1)번 식은 $x^i$ 값이 아주 작게 움직였을때, 함수 $f$의 결과값이 얼만큼 움직이는지를 나타내고있다.

Numerical 접근에선 크게 두가지 문제점이 존재한다. 첫번째 문제는 극한 (limit) 정의를 코드로 구현할 때 발생하는 오차 문제 (rounding error) 이다. 이는 아주 작은 $h$ 값을 컴퓨터의 floating point로 표현할 때 발생하는 물리적인 한계에서 비롯된 문제이다. 관심이 있는 독자들은 링크를 통해 더 자세한 내용을 확인하자.

두번째 문제는 해당 접근법이 $O(n)$ 만큼의 연산, 즉 각 가중치와 편향 값에 대한 개별적인 연산을 수행해야 한다는 점이다. 이는 수십만개의 가중치와 편향 값을 학습하는 신경망 네트워크에 지나친 연산 부담을 줄 수 있다.

b. Symbolic

Symbolic 접근은 사람이 실제 미분 연산시에 사용하는 연산 규칙 (예를 들어 $\sin (x)$ 의 미분값은 $\cos (x)$) 을 기반으로 편미분을 구하는 방식이다. 해당 접근법에서 손실함수는 가중치와 편향의 수식으로 표현되며, 연산 규칙을 그 기반으로 하기에 numerical 접근법의 오차 문제를 해결한다. 대표적인 예시로 SymPy 패키지가 있다.


Fig 1. SymPy 패키지 적분 연산 사용 예시

(고등학생때 알았더라면…!)

얼핏 생각하기에 타당해 보이는 symbolic 접근 또한 역전파 적용이 어려운 이유가 존재한다. 가장 대표적인 문제는 expression swell 인데, 손실함수의 수식보다 그 미분 수식이 기하급수적으로 복잡해지는 문제이다. 다음 예시와 함께 미분의 곱 규칙을 생각해보자.

$$ h(x) = f(x)g(x) \newline h’(x) = f’(x)g(x) + f(x)g’(x) \newline $$

$f(x)$를 다음과 같이 정의하면 $h’(x)$는 더욱 복잡해진다.

$$ f(x) = u(x)v(x) \newline h’(x) = (u’(x)v(x) + u(x)v’(x))g(x) + u(x)v(x)g’(x) \newline $$

이는 한가지 예시에 불과하고, 미분 수식의 복잡성은 손실함수의 수식과 비례하지 않기 때문에 해당 접근은 numerical 접근의 $O(n)$ 연산을 뛰어넘는 연산 부담을 네트워크에 줄 가능성이 있다. 또한 미분 연산의 대상이 항상 특정 수식으로 표현되어야 한다는 제약을 가지고 있다.

c. Automatic

Automatic 접근은 수식에 기반하는 대신, 덧셈, 곱셈과 같은 개별적인 연산자 그래프 (DAG) 를 생성하여 미분 연산 과정을 가장 작은 단위에서 수행하는 접근법이다. 다음 그래프를 참고하자.


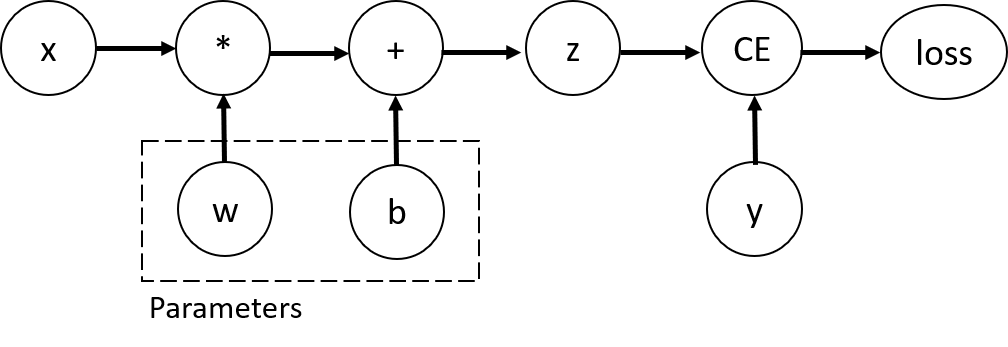Fig 2. 단일 뉴런의 Autograd DAG 예시

여기서 $w$는 가중치, $b$는 편향, $z$는 활성함수를 나타낸다 (편의를 위해 loss 또한 $L$로 지칭하겠다). 위 그래프에서 가중치 $w$의 편미분값, $\frac{\delta L}{\delta w}$ 값을 연산한다고 가정해보자. 우선 CE (Cross Entropy) 함수의 미분식을 통해 $\frac{\delta L}{\delta z}$ 를 구한 후, $z$ 함수의 미분식을 사용해 구한 $\frac{\delta z}{\delta w}$를 $\frac{\delta L}{\delta z}$ 에 곱해줌으로서 $\frac{\delta L}{\delta z} \cdot \frac{\delta z}{\delta w} = \frac{\delta L}{\delta w}$를 연산할 수 있다. 더 작은 단위의 (레이어가 아닌 연산자 단위) 역전파라 생각해도 무방할 듯 하며, 복잡해 보이지만 편미분의 정의를 되새기며 기호와 그래프를 유심히 따라가면 그 의미가 전달 될 것이라 생각한다.

Jacobian-Vector Products (JVPs)

위 Fig 3. 의 예시에서는 2개의 input $w$, $b$와, 1개의 output $L$에 대한 연산자 그래프를 살펴보았다. Input의 개수가 $n$이고, output의 개수가 $m$인 경우는 어떨까? 해당 연산자 그래프에 대해서 다음과 같은 편미분 매트릭스 (야코비 행렬, Jacobian Matrix)를 구할 수 있을 것이다.

(여기서 $x$는 input을, $f$는 output을 뜻하고 있다)

$$ \begin{equation*} J_{f} = \begin{bmatrix} \frac{\delta f_1}{\delta x_1 } & \frac{\delta f_2}{\delta x_1 } & \cdots & \frac{\delta f_m}{\delta x_1 } \newline \frac{\delta f_1}{\delta x_2 } & \frac{\delta f_2}{\delta x_2 } & \cdots & \frac{\delta f_m}{\delta x_2 } \newline \vdots & \vdots & \ddots & \vdots \newline \frac{\delta f_1}{\delta x_n } & \frac{\delta f_2}{\delta x_n } & \cdots & \frac{\delta f_m}{\delta x_n } \newline \end{bmatrix} \end{equation*} $$

야코비 행렬은 모든 input과 output의 조합에 대한 편미분 값을 가지고 있으며, 각 열에는 output $f_i$, 행에는 input $x_j$에 속하는 값이 정렬되어있다. 특정 output 값 $f_i$에 대한 모든 input $x$의 편미분 벡터를 구하기 위해서는 다음과 같이 적합한 벡터 $r$을 곱해주어야 한다.

$$ \begin{equation*} \frac{\delta f_i}{\delta x} = J_f r = \begin{bmatrix} \frac{\delta f_1}{\delta x_1 } & \frac{\delta f_2}{\delta x_1 } & \cdots & \frac{\delta f_m}{\delta x_1 } \newline \frac{\delta f_1}{\delta x_2 } & \frac{\delta f_2}{\delta x_2 } & \cdots & \frac{\delta f_m}{\delta x_2 } \newline \vdots & \vdots & \ddots & \vdots \newline \frac{\delta f_1}{\delta x_n } & \frac{\delta f_2}{\delta x_n } & \cdots & \frac{\delta f_m}{\delta x_n } \newline \end{bmatrix} \cdot \begin{bmatrix} 1 \newline 0 \newline \vdots \newline 0 \newline \end{bmatrix} = \begin{bmatrix} \frac{\delta f_1}{\delta x_1 } \newline \frac{\delta f_1}{\delta x_2 } \newline \vdots \newline \frac{\delta f_1}{\delta x_n } \newline \end{bmatrix} \end{equation*} $$

Autograd 사용법

PyTorch의 Autograd 패키지는 이러한 야코비 행렬을 연산해주는 기능을 가지고있다. 우선 input 벡터인 $x$를 지정하는 법을 알아보자.

requires_grad 파라미터

Input 벡터로 사용하고자 하는 tensor를 최초로 생성할때는 requires_grad 파라미터를 True로 설정해야한다. 다음 예시를 확인하자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


 import torch

 x = torch.randn(3, requires_grad=True)
 print(x)
 >>> tensor([-1.0475, 0.2038, 0.2971], requires_grad=True)

 y = x + 2
 print(y)
 >>> tensor([1.6828, 2.3467, 2.6648], grad_fn=<AddBackward0>)

 z = y * y * 2
 print(z)
 >>> tensor([1.5855, 2.3060, 2.3540], grad_fn=<MulBackward0>)

 z = z.mean()
 print(z)
 >>> tensor(8.9153, grad_fn=<MeanBackward0>)

x tensor 생성 시 requires_grad 파라미터를 True로 설정할 경우, x를 변수로 사용한 함숫값 y, z tensor에 grad_fn 이라는 미분 함수가 내제되어있는 것을 확인할 수 있다. 이는 언급했던 연산자 그래프의 노드에 해당하며, 편미분 연산시에는 이러한 노드를 순차적으로 되돌아가며 결과값을 연산하게된다.

backward() 함수

앞선 예시에서 최종 함숫값인 z에 다음과 같이 backward 함수를 호출할 시, 역전파에 필요한 편미분값 $\frac{\delta z}{\delta x}$ 를 x.grad 속성을 통해 확인할 수 있다.

1
2
3
4


 z.backward() # dz/dx

 print(x.grad)
 >>> tensor([0.0160, 3.3650, 4.5153])

이 경우에는 z가 단일값이기 때문에 야코비 행렬이 그대로 리턴되었다. z가 단일값이 아닌 벡터일때는 어떻게 해야할까? 결과값이 매트릭스이기 때문에 어떤 $z$값에 대한 편미분을 구해야 하는지가 명확하지 않다. 이러한 경우 앞선 예시에 사용된 벡터 $r$을 매개변수로 집어넣어야 한다. 다음 예시를 확인하자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


 x = torch.randn(3, requires_grad=True)
 y = x + 2
 z = y * y * 2

 z.backward()
 >>> RuntimeError: grad can be implicitly created only for scalar outputs.

 r = torch.tensor([1.0, 0, 0], dtype=torch.float32)
 z.backward(r)
 print(x.grad)
 >>> tensor([5.0823, 0.0000, 0.0000])

대부분의 경우 편미분 연산은 단일값인 손실함수 $L$에 대해 이루어지기 때문에 backward 함수 사용 시 별도의 매개변수는 사용하지 않게된다. 관련 내용에 궁금증이 남는다면 본 영상을 참고하자.