PyTorch Deep Learning - Backpropagation & Gradient Descent

소개

머신러닝과 분야에서 가장 뼈대가 되는 수학 공식은 경사하강이다. 왜일까? SVM, 선형회귀, 신경망과 같은 통상적인 예측 모델은 모두 다른 방식으로 예측값 $\tilde{Y}$ 를 예측하지만, 이 모든 모델의 정확도를 향상하는 학습과정에서는 언제나 알고리즘에 알맞는 경사하강 공식을 사용하기 때문이다. 구체적으로 경사하강이란 모델의 성능을 더 나은 방향으로 개선시킬 수 있도록 조절 가능한 모델의 변수를 업데이트하는 과정을 가르킨다.

모든 경사하강 과정은 그에 알맞는 기울기 값, 즉 gradient 를 필요로하며, 이는 모델의 변수가 어떤 방향으로 (음수 또는 양수) 움직일때 성능이 개선되는지에 대한 정보를 제공한다. 신경망의 경우, 이러한 변수 별 gradient 값을 연산하기 위해 오차역전파라는 방법을 사용한다. 해당 글에서는 PyTorch 프레임워크를 사용하여 오차역전파를 수행하고, 신경망 모델의 경사하강을 구현하기까지의 과정을 실습해보고자 한다.

Autograd 복습

PyTorch Deep Learning - 2. Autograd 글에서 살펴보았듯 신경망의 gradient 값을 도출하기 위해서는 역전파를 수행해야하며, 이는 PyTorch 라이브러리의 autograd 기능을 활용해 구현이 가능하다.


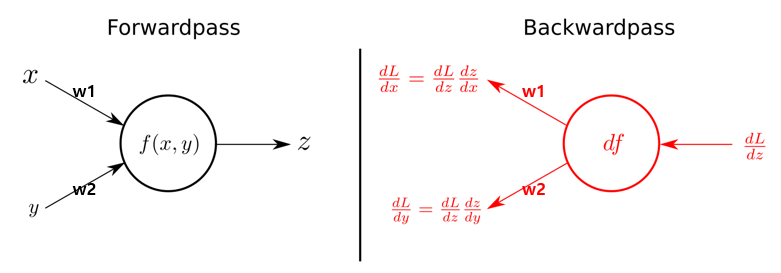Fig 1. 단일 뉴런의 역전파 과정

$x = 1$ 의 인풋을 활용해 $y = 2$ 를 예측하는 단일 뉴런 모델의 역전파 과정을 PyTorch 로 구현한 코드는 다음과 같다. 이 경우 가중치인 $w$ 의 초기값이 최적치에 비해 낮기 때문에 gradient 는 음수가 되어야 한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


 import torch

 x = torch.tensor(1.0)
 y = torch.tensor(2.0)

 w = torch.tensor(1.0, requires_grad=True)

 # forward pass and compute the loss
 y_hat = w * x
 loss = (y_hat - y)**2
 print(loss)
 >>> tensor(1., grad_fn=<PowBackward0>)

 # backward pass
 loss.backward()
 print(w.grad)
 >>> tensor(-2.)

경사하강

경사하강이란 연산한 gradient 의 반대방향, 즉 손실함수를 낮추는 방향으로 모델의 파라미터를 업데이트하는 과정을 일컫는다. 아래 그림에서 start 지점의 gradient, 즉 미분값은 경사가 상대적으로 큰 양수값이며, 따라서 손실함수 $J(W)$ 를 최소화하기 위해 반대방향인 음수값으로 $w$ 를 업데이트하는 과정을 확인할 수 있다. 아직 gradient가 어떻게 손실함수를 낮추는 방향을 제시하는가에 대한 직관적인 이해가 이루어지지 않는다면 1, 2 비디오를 참고하길 바란다. 또한 해당 글은 Momentum, RMSProp, Adam 등 다양한 경사하강법을 소개하고있다.


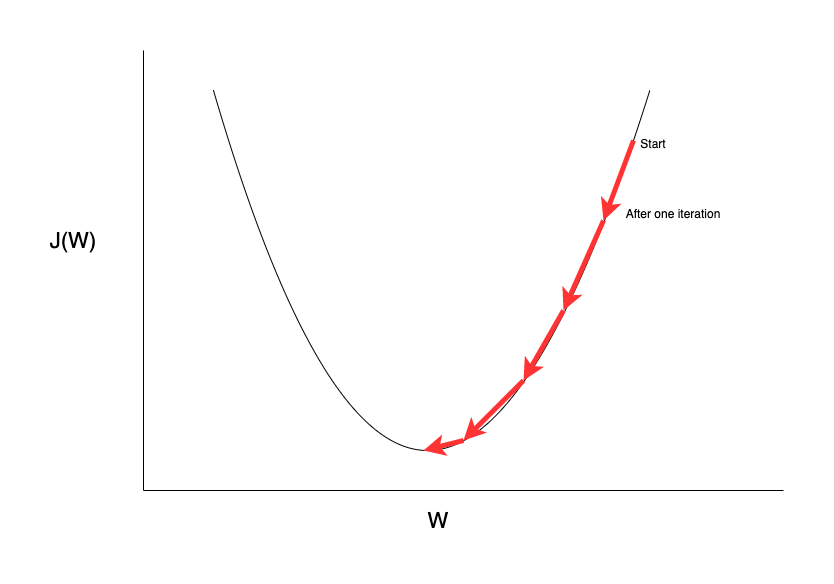Fig 2. 단일 뉴런의 역전파 과정

신경망 모델에서 경사하강을 수행하기 위해서는 다음과 같은 과정을 순차적으로 수행해야한다.

Prediction: 현재 파라미터 값을 사용한 예측
Loss Computation: 손실값 계산
Gradients Computation: 예측값을 기반으로 한 gradient 연산
Parameter updates: gradient 값을 기반으로 한 파라미터 업데이트

Manual 접근법

우선 PyTorch 라이브러리 없이 Numpy 만으로 이와 같은 손실함수 과정을 구현하는 코드를 살펴보자. 해당 코드의 gradient 는 MSE 함수에 대한 미분값을 별도로 계산한 것이며, 다음 식을 기반으로 하고있다.

$$ \frac{\delta J}{\delta w} = \frac{1}{N} \cdot 2x (wx - y) $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


 import numpy as np

 X = np.array([1, 2, 3, 4], dtype=np.float32)
 Y = np.array([2, 4, 6, 8], dypte=np.float32)

 w = 0.0

 # model prediction
 def forward(x):
    return w * x
 
 # loss = MSE
 def loss(y, y_pred):
    return ((y_pred - y) ** 2).mean()

 # gradient
 def gradient(x, y, y_pred):
    return np.dot(2 * x, y_pred - y).mean()

 # training
 learning_rate = 0.01
 n_iters = 10

 for epoch in range(n_iters):
    y_pred = forward(X)
    l = loss(Y, y_pred)
    dw = gradient(X, Y, y_pred)

    # update weights
    w -= learning_rate * dw

Autograd 활용

다음 코드는 상단 경사하강 과정의 Gradients Computation 단계에서 수식이 아닌 Autograd 패키지의 자동미분 기능을 사용한 것이다. gradient 함수가 사라지고, 학습과정의 코드 변화를 확인할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


 import torch

 X = torch.tensor([1, 2, 3, 4], dtype=torch.float32)
 Y = torch.tensor([2, 4, 6, 8], dypte=torch.float32)

 # requires_grad 매개변수 설정
 w = torch.tensor(0.0, dtype=torch.float32, requires_grad=True)

 # model prediction
 def forward(x):
    return w * x
 
 # loss = MSE
 def loss(y, y_pred):
    return ((y_pred - y) ** 2).mean()

 # training
 learning_rate = 0.01
 n_iters = 10

 for epoch in range(n_iters):
    y_pred = forward(X)
    l = loss(Y, y_pred)

    # backward pass
    l.backward()

    # update weights
    with torch.no_grad():
        w -= learning_rate * w.grad

    # reset gradient
    w.grad.zero_()